Produit une grille bidimensionnelle. Utile pour la visualisation tridimensionnelle de fonctions à deux variables ou de fonctions à arguments à valeur complexe.

Syntaxe

MeshGrid(X, Z)

La syntaxe de la fonction MeshGrid se compose des éléments suivants :

Remarques

Le résultat a toujours la structure de données Liste.

A partir de deux séries de données, X avec la longueur N et Z avec la longueur M la fonction produit une liste avec deux entrées portant le même nom X et Z. Toutefois, les entrées résultantes dans la liste sont désormais des matrices composées de N lignes et M colonnes, qui sont formées en répliquant les arguments de la fonction X ou Z. Les unités des matrices de résultats correspondent aux unités des arguments individuels.

Le résultat peut être interprété comme une grille rectangulaire bidimensionnelle avec N x M points de grille comme suit : Par exemple, sont spécifiées les séries de données X comme {1, 2, 3, 4} dans le sens horizontal et les séries de données Z comme {7, 8, 9} dans le sens vertical. La grille délimitée par X et Zcomprend désormais les coordonnées (1, 7), (2, 7), (3, 7), (4, 7), ..., (1, 9), (2, 9), (3, 9), (4, 9) :

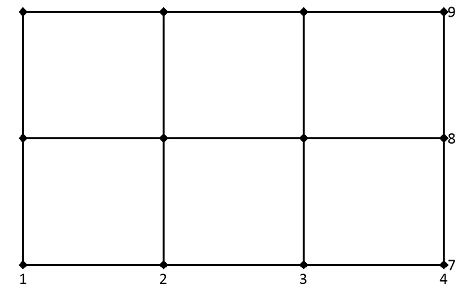
Les coordonnées des différents points de la grille sont obtenues par élément à partir des deux matrices portant les mêmes noms :

La fonction MeshGrid appliquée aux deux séries de données, aboutit maintenant à la liste constituée des matrices portant le même nom X (premier élément de la liste) et Z (deuxième élément de la liste).

La fonction est généralement utilisée pour l'affichage tridimensionnel des fonctions y = f(x, z) de deux variables sur une grille rectangulaire à deux dimensions. En particulier, les fonctions y = f(z) = f(z1, z2) avec des arguments à valeur complexe z = z1 + i * z2 peut être calculée et affichée sur le plan complexe.

Disponible dans

FlexPro Basic, Professional, Developer Suite

Exemples

Dim x = {1, 2, 3, 4}
Dim z = {7, 8, 9}
Dim grid = MeshGrid(x, z)
Dim y = grid.["X"]^2 - grid.["Z"] // = grid.[0]^2 - grid.[1]
Signal(y, x, z)

Exemple 1 : Procédure de calcul des fonctions à deux variables

Calcule la fonction y = x^2 - z délimitant la grille à l'aide des séries de données {1, 2, 3, 4} (dans la direction X) et {7, 8, 9} (dans la direction Z) :

Dim x = Series(-4, 4, 0.01)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = ArcTan2(grid.["Z"], grid.["X"])
Signal(y, x, z)

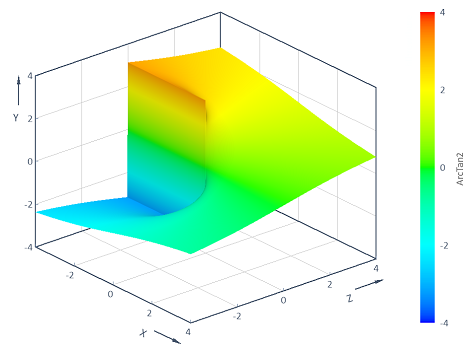
Exemple 2 : Visualisation de la fonction ArcTan2 avec 2 variables

Calcule la fonction ArcTan2 y = f(x, z) = ArcTan2(z, x) à travers la plage (x, z) bidimensionnelle [-4, 4] x [-4, 4]. La visualisation dans un graphique de contour 3D donne les résultats suivants :

Dim x = Series(-16, 16, 0.04)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = Sinc(Sqrt(grid.["X"]^2 + grid.["Z"]^2))
Signal(y, x, z)

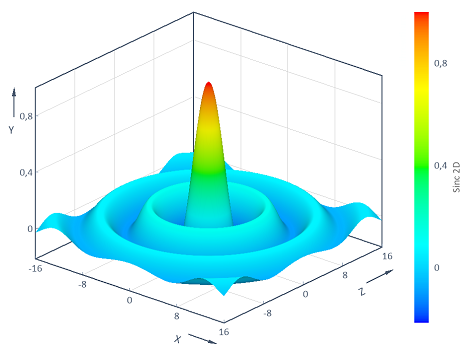
Exemple 3 : Visualisation de la fonction Sinc en 2D

Calcule la fonction Sinc bidimensionnelle y = f(x, z) = Sinc(Sqrt(x^2 + z^2)) à travers la plage (x, z) bidimensionnelle [-16, 16] x [-16, 16]. La visualisation dans un graphique de contour 3D donne les résultats suivants :

Dim z1 = Series(-6, 6, 0.02)
Dim z2 = z1
Dim grid = MeshGrid(z1, z2)
Dim y = Real(Log(grid.[0] + 1i * grid.[1]))
Signal(y, z1, z2)

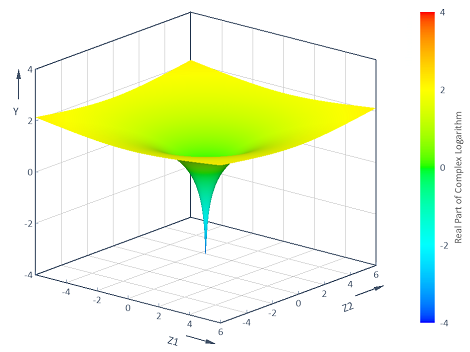
Exemple 4 : Visualisation des fonctions avec des arguments complexes

Calcule la partie réelle du logarithme complexe y = f(z1, z2) = Real(Log(z1 + i* z2)) à travers le plan (z1, z2) complexe [-6, 6] x [-6, 6]. La visualisation dans un graphique de contour 3D donne les résultats suivants :

Arguments x, z
Dim xMatrix = x # NumberOfRows(z)
Dim zMatrix = TransposeMatrix(z # NumberOfRows(x))
List("X", xMatrix, "Z", zMatrix)

Exemple 5 : Code FPScript équivalent

Le code FPScript suivant produit le même résultat que la fonction MeshGrid.

Voir aussi

Fonction ArcTan2

Fonction List

Fonction NumberOfColumns

Fonction NumberOfRows

Fonction Reshape

Fonction Shape

Fonction TransposeMatrix

Opérateur List

Opérateur List Element