Multiplie les matrices par des vecteurs et des matrices dans toutes les combinaisons.

Syntaxe

MatrixMultiplication(A, B)

La syntaxe de la fonction MatrixMultiplication se compose des éléments suivants :

Remarques

L'unité du résultat est la même que le produit des unités de A et B. Les arguments A et B fournissent les matrices ou vecteurs à multiplier. Dans ce cas, les matrices sont fournies sous forme de matrices de données dont les séries de données correspondent aux lignes. Les vecteurs sont fournis sous forme de séries de données.

Pour les arguments complexes, une multiplication complexe a lieu et le résultat est également complexe. Le résultat a toujours le même type de données que les arguments. Si les arguments ont des types de données différents, ceux-ci sont adaptés les uns aux autres de manière à ce qu'il n'y ait pas de perte de résolution dans le résultat, c'est-à-dire que les résolutions inférieures sont converties en résolutions supérieures, les nombres entiers en valeurs à virgule flottante et les nombres réels en nombres complexes.

La multiplication complexe est définie comme (a, b) * (c, d) = (a * c - b * d, a * d + b * c).

Le résultat a le même type de données que l'argument converti, le cas échéant. Les opérations suivantes sont effectuées :

Vecteur avec vecteur : Le produit scalaire des deux vecteurs A et B est formé.

Exemple pour les vecteurs à trois éléments :

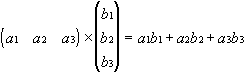
Matrice avec vecteur : Chaque ligne de la matrice A est multipliée vectoriellement par le vecteur B. Le nombre de lignes dans la matrice A doit correspondre au nombre d'éléments dans le vecteur B.

Exemple pour une matrice 3x3 A et vecteur B avec trois éléments :

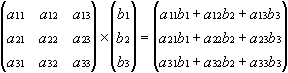
Vecteur avec matrice : Chaque colonne de la matrice B est multipliée vectoriellement par le vecteur A où le nombre de colonnes de la matrice doit correspondre au nombre d'éléments du vecteur.

Exemple pour une matrice 3x3 et un vecteur à trois éléments :

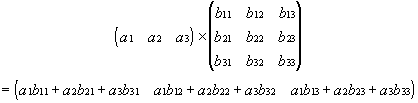
Matrice avec matrice : Chaque ligne de la matrice A est multipliée vectoriellement par chaque colonne de la matrice B. Le nombre de lignes dans la matrice A doit correspondre au nombre de colonnes dans la matrice B.

Exemple pour deux matrices 3x3 :

Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste.

Remarque        Notez que les séries de données dans la matrice de données sont interprétées comme les lignes de la matrice, bien qu'elles soient affichées comme des colonnes dans la fenêtre des ensembles de données. Cet assignement est nécessaire pour que l' Opérateur Index puisse être appliqué pour les matrices dans l'ordre défini en Algèbre Linéaire où la première valeur d'indice spécifie la ligne et la seconde la colonne.

Disponible dans

FlexPro Basic, Professional, Developer Suite

Exemples

Voir aussi

Fonction InverseMatrix

Fonction TransposeMatrix