Les filtres LOESS et LOWESS sont des méthodes de lissage très populaires qui utilisent une fonction de régression pondérée localement.

Cette méthode utilise une fonction de pondération ayant pour effet que l'influence d'une valeur voisine sur la valeur lissée à une certaine position diminue avec leur distance à cette position. Les valeurs aberrantes sont pondérées plus faiblement par rapport aux autres méthodes. L'important est de sélectionner la largeur de lissage qui rend le nombre de valeurs observées utilisé pour le calcul d'un point. En outre, deux types de pondération sont utilisés : la pondération de proximité et la pondération robuste.

Étape 1 :

Dans la première étape de la méthode, on détermine la plage des points à inclure. Le nombre n de ces points est spécifié. Plus cette valeur est grande, plus la courbe adaptée sera lisse au final. La plage est déterminée de telle sorte qu'exactement n valeurs, y compris le point sélectionné lui-même, se trouvent dans la plage, et que le point sélectionné se trouve au centre de la plage sélectionnée. Il est donc possible que le nombre de points à gauche et à droite soit différent. Par exemple, la première valeur n'a que des points voisins à droite.

Étape 2 :

Dans la deuxième étape, la pondération est établie pour le lissage par régression pondérée localement. La fonction de pondération est définie par :

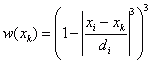
pour k = 1,...,N

di est la distance entre xi et le Nième point voisin. La fonction de pondération est symétrique. La plus grande valeur est atteinte au point xi. La valeur 0 est aux limites de la gamme.

Étape 3 :

Le lissage de la régression va maintenant avoir lieu. Une fonction de régression linéaire basée sur la méthode des moindres carrés est estimée pour la procédure LOWESS. La procédure LOESS, quant à elle, utilise une fonction quadratique.

Les paramètres sont calculés de telle sorte que la fonction suivante soit minimisée :

LOWESS :

LOESS :

Étape 4 :

Seules quelques valeurs observées sont incluses pour estimer la fonction de régression linéaire dans les plages individuelles. Il est toujours possible dans ce cas que la fonction de régression estimée soit plus ou moins fortement influencée par des valeurs aberrantes potentielles. Par conséquent, des pondérations robustes sont déterminées dans une quatrième étape de la procédure. Pour déterminer les pondérations, on calcule les résidus des valeurs estimées jusqu'à ce point et la médiane qui en résulte.

Les pondérations robustes sont calculées à l'aide de la formule suivante :

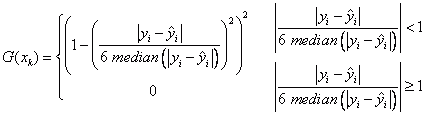
La pondération robuste est de 0 si un résidu est supérieur ou égal à 6 m (m = médiane des résidus). Cela permet d'éliminer les valeurs aberrantes.

Les pondérations robustes, multipliées par les pondérations de proximité, sont utilisées pour réestimer une fonction de régression linéaire dans les plages individuelles :

LOWESS :

LOESS :

Le résultat est une série de nouvelles valeurs lissées. La procédure peut être répétée plusieurs fois. Plus le nombre d'itérations est élevé, plus l'ajustement de la courbe est précis ; toutefois, si le nombre d'itérations est déjà élevé, l'augmenter n'apportera pratiquement aucune amélioration visible.

Références

•Cleveland, W.S. (1979). Robust Locally Weighted Regression and Smoothing Scatterplots. Journal of the American Statistical Association, Vol. 74, pp. 829-836.