Integral (FPScript)
Calcule l'intégrale.
Syntaxe
Integral(Signal [ , Mode = INTEGRAL_TRAPEZOIDAL ])
ou
Integral(Amplitude, Time [ , Mode = INTEGRAL_TRAPEZOIDAL ])
La syntaxe de la fonction Integral se compose des éléments suivants :
Section |
Description |
||||||||
|---|---|---|---|---|---|---|---|---|---|
Signal |
Le signal dont l'intégrale est calculée. Si l'argument est une série de données ou une matrice de données, alors 1 est utilisé comme l'incrément dX pour l'intégration. Les structures de données autorisées sont Séries de données, Matrice de données, Signal, Série de signaux et Série de signaux avec composante X bidimensionnelle. Tous les types de données numériques sont autorisés. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||||
Amplitude |
La composante Y du signal à intégrer. Si vous spécifiez un signal, alors sa composante Y est utilisée. Les structures de données autorisées sont Séries de données, Matrice de données, Signal, Série de signaux et Série de signaux avec composante X bidimensionnelle. Tous les types de données numériques sont autorisés. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||
Time |
La composante X du signal à intégrer. Si vous spécifiez un signal, alors sa composante Y est utilisée. Les structures de données autorisées sont Séries de données, Matrice de données, Signal, Série de signaux et Série de signaux avec composante X bidimensionnelle. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||||
Mode |
Pour le calcul discret de l'intégrale, on utilise des formules d'approximation avec différents ordres de précision. L'argument Mode peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut INTEGRAL_TRAPEZOIDAL . |
Remarques
Le résultat est toujours du type de données Virgule flottante de 64 bits.
L'unité du résultat est la même que le produit des unités des composantes Y et X de Signal. Les valeurs sont converties en valeurs à virgule flottante 64 bits avant que le calcul ne soit effectué. Pour les matrices de données et les séries de signaux, le calcul s'effectue colonne par colonne. Les composantes X et Z, si elles sont présentes, sont copiées dans le résultat sans modification. Le résultat peut être considéré comme une fonction primitive du signal.
L'intégrale est calculée en mode INTEGRAL_TRAPEZOIDAL à l'aide de la formule trapézoïdale (au moins deux points de données sont nécessaires) :
La règle du trapèze peut également être appliquée à des ensembles de données échantillonnés non équidistants.
L'intégrale est calculée en mode INTEGRAL_SIMPSON avec l'aide de la règle de Simpson. La règle de Simpson exige des ensembles de données échantillonnés de façon équidistante (au moins trois ensembles de données sont nécessaires) :
L'intégrale est calculée en mode INTEGRAL_CUBIC à l'aide d'une formule d'intégration cubique. Cette règle d'intégration est la forme centralisée de la règle d'intégration d'Adam (formule d'interpolation d'Adams ou intégrateur Ngo, voir [4]. La règle exige également des ensembles de données échantillonnés de manière équidistante (au moins quatre ensembles de données sont nécessaires) :
Dans tous les modes, l'intégrale est définie à la limite gauche I[0] comme étant 0. Dans le cas de la règle de Simpson et de la règle d'intégration cubique, il n'y a pas assez de points d'échantillonnage pour la formule d'approximation aux limites I[1] (et pour la règle cubique également pour la limite droite I[N]). On utilise alors des règles de calcul qui ont le même ordre de précision (semblable à [2, page 98]).
Remarque En général, les dispositions suivantes s'appliquent : Plus l'ordre de précision est élevé lors du choix de la règle d'intégration, plus la précision est grande dans la détermination de l'intégrale pour les ensembles de données lisses (non bruyantes). Cependant, si les ensembles de données sont bruyants, l'erreur numérique sera pire dans la détermination de l'intégrale si une règle d'intégration d'ordre supérieur est utilisée. Le mode d'intégration doit donc être choisi en fonction du bruit/la fluidité de l'ensemble de données sous-jacent.
D'autre part, si l'on s'intéresse au spectre des fréquences, il est utile de considérer les règles d'intégration comme des filtres numériques (voir aussi [1] ou [3, section 7.2]). Les règles d'intégration ont la réponse d'amplitude suivante. L'intégrateur idéal est également affiché (profil de filtre de l'intégration continue) :
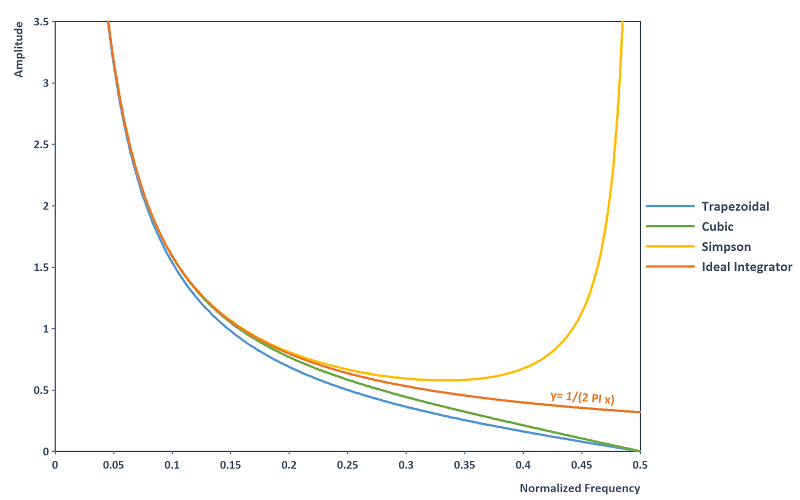
Observation : La règle trapézoïdale et la règle d'intégration cubique ont des caractéristiques naturelles de passe-bas et suppriment les bruits à haute fréquence en sous-estimant l'intégrateur idéal. La règle d'intégration cubique présente une approximation de la réponse d'amplitude de l'intégrateur idéal plus précise que la règle trapézoïdale dans tout le domaine des fréquences. La règle de Simpson fournit l'approximation de la réponse d'amplitude la plus précise de l'intégrateur idéal dans le domaine des fréquences jusqu'à 0,25, mais diverge dans le domaine de la limite de Nyquist 0,5. Le bruit à haute fréquence est ainsi amplifié en utilisant la règle de Simpson. Il convient de noter que toutes les règles de rapprochement ont une réponse de phase constante de -90 degrés et correspondent donc à la phase de l'intégrateur idéal.
Disponible dans
FlexPro View, Basic, Professional, Developer Suite
Exemples
Integral({1,2,3,2,1}, {0,1,2,3,4})
Utilise la règle trapézoïdale pour calculer l'intégrale {0, 1,5, 4, 6,5, 8} des séries de données spécifiées comme argument.
Integral(Signal)[-1]
Calcule l'aire sous la courbe d'un signal. Pour ce faire, la dernière valeur doit être extraite du résultat.
Integral(Detrend(Signal))
Intègre un signal périodique et supprime la valeur moyenne au préalable. Dans ce cas, la fonction Detrend a été utilisée pour supprimer la composante continue ou une tendance linéaire ou adaptative du signal avant l'intégration. Raison : Lorsque vous intégrez des signaux périodiques dont la moyenne n'est pas nulle, la courbe intégrée s'éloigne par accumulation de la valeur moyenne dans le signal. L'illustration suivante clarifie la situation :
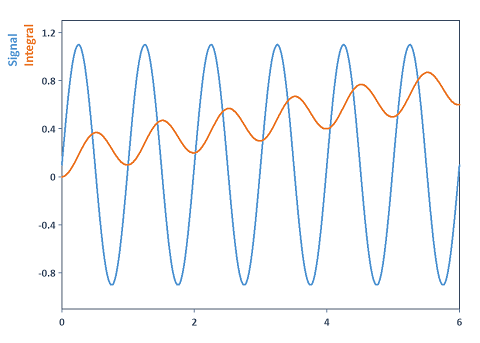
Integral(DCRemovalFilter(Signal))
Intègre un signal et supprime au préalable la dérive ou le décalage (composante continue). Pour supprimer la dérive ou le décalage, la fonction DCRemovalFilter a été utilisée à la place de la fonction Detrend. Raison : La raison de cette dérive du signal après l'intégration n'est pas seulement l'accumulation du décalage pendant l'intégration, mais aussi la réponse d'amplitude inversement proportionnelle de l'intégrateur à la fréquence. Cela amplifie le bruit à des fréquences proches de l'offset (composante continue) et l'intégration l'élève à des valeurs arbitrairement élevées. La courbe intégrée dérive alors. Pour éviter cette dérive, il ne suffit pas de soustraire la moyenne, mais les fréquences proches de la composante continue doivent également être coupées à l'aide d'un filtre passe-haut. L'illustration suivante clarifie la situation (à titre d'exemple, un des signaux d'accélération des fichiers d'exemple FlexPro sous C:\Users\Public\Documents\Weisang\FlexPro a été intégré) :
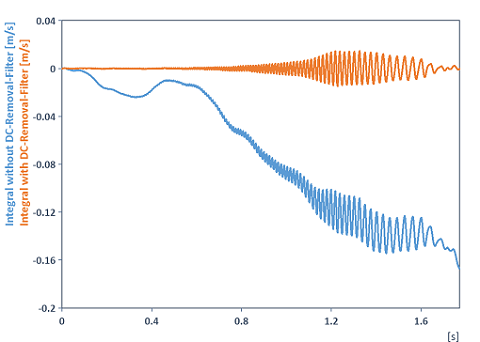
Dim filterCoef = List("b", {1/3, 4/3, 1/3}, "a", {1, 0, -1})
AmplitudeResponse(filterCoef)
Calcule la réponse en amplitude du filtre Simpson à l'aide de la fonction AmplitudeResponse.
Dim x = Series(0, 6, 0.5)
Integral(Signal(2.2 + 6.2*x + 12.6*x^2 - 2*x^3, x), INTEGRAL_CUBIC)
Calcule l'intégrale d'un polynôme du troisième degré aux x points d'échantillonnage. Le résultat est conforme à l'intégrale exacte Signal(2.2*x + 3.1*x^2 + 4.2*x^3 - 0.5*x^4, x).
Dim x = (30, 1, 0.1)
Dim f = Signal(50 * 1/x, x)
Dim integralExact = Signal(50 * log(x), x)
Absolute(Integral(f, INTEGRAL_TRAPEZOIDAL)[-1] - integralExact[-1])
Détermine l'erreur pour le mode INTEGRAL_TRAPEZOIDAL lors du calcul de l'intégrale numérique de la fonction lisse f = 50 * 1 / x. L'erreur est proportionnelle à 0,01. En revanche, si INTEGRAL_SIMPSON est sélectionné, cela donne une erreur proportionnelle à 0,001. En sélectionnant INTEGRAL_CUBIC renvoie la plus grande précision avec une erreur proportionnelle à 0,0001.
Voir aussi
Fonction SavitzkyGolayDerivative
Analyse du signal - Objet d'analyse
Littérature
[1] Tilman Butz: Fourier Transformation for Pedestrians. Springer Berlin Heidelberg New York,http://www.springer.com/de/book/9783319169842,2015.ISBN 3-540-23165-X.
[2] C. Woodford, C. Phillips: Numerical Methods with Worked Examples. Chapman and Hall, 2-6 Boundary Row, London SE1 8HN, UK,1997.ISBN 0-412-72150-3.
[3] Richard G. Lyons: Understanding Digital Signal Processing (3rd Edition). Prentice Hall,2011.ISBN 0-13-702741-9.
[4] N. Q. Ngo: A new approach for the design of wideband digital integrator and differentiator. Dans: IEEE Trans. Circuits Syst. II, Exp. Briefs, Vol. 53, No. 9, Pages 936-940. Prentice Hall,2006.
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations