Fenêtre d’observation des données
Les fenêtres d'observation de données sont utilisées pour réduire les fuites spectrales dans les spectres de Fourier.
Fenêtres d'observation de données de Fourier à largeur fixe
Les fenêtres d'observation de données de forme fixe suivantes sont disponibles dans FlexPro. La caractérisation des fenêtres s'effectue dans le domaine des fréquences. La valeur dB indique l'atténuation du premier lobe latéral par rapport au lobe principal. Les fuites diminuent lorsque l'atténuation augmente. Le terme "rolloff" décrit la décroissance des lobes latéraux. L'étalement spectral de la fuite diminue lorsque l'atténuation augmente. La valeur W (Width) décrit la largeur unilatérale du maximum du lobe principal en tant que multiple du maximum du lobe principal de la fenêtre rectangulaire. La résolution spectrale diminue lorsque la largeur augmente.
Fenêtres |
Calculé en utilisant |
|---|---|
Rectangulaire -13dB W=1 (pas de fenêtrage) |
1,0 |
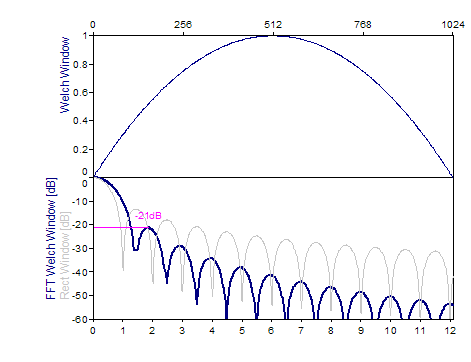
Welch -21dB W=1,4 |
1.0-(((n-1)-2*i)/(n-1)*((n-1)-2*i)/(n-1)), i=0..n-1 |
Sinus -23dB W=1,5 |
sin(π*i/(n-1)), i=0..n-1 |
BiSquare -28dB W=1,8 (Connes) |
1.0-(absolute(i-0.5*n+0.5))²/(0.5*n-0.5)²)², i=0..n-1 |
Bartlett -27dB W=2 |
2*i/(n-1), i=0..(n-1)/2 2-2*i/(n-1), i=(n-1)/2+1..n-1 |
0.5-0.5*cos(2*π*i/(n-1)), i=0..n-1 |
|
TukeyHann -37dB W=2 |
0.25*Dirichlet(2*(i/(n-1))-1.0-0.5)+(1.0-2.0*0.25)*Dirichlet(2*(i/(n-1))-1.0)+0.25*Dirichlet(2*(i/(n-1))-1.0+0.5), i=0..n-1 mit Dirichlet(q)=sin((2*π+0,5)*q)/(2*π*sin(0,5*q)) |
Bartlett modifié -39dB W=2,3 |
(sin(π*(2*(i/(n-1))-1)))²/(2*π*sin((i/(n-1))-0.5))², i=0..n-1 |
0.53836-0.46164*cos(2*π*i/(n-1)), i=0..n-1 |
|
Cos3 Maximum Rolloff -47dB W=3 |
0.375-0.5*cos(2*π*i/(n-1))+0.125*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman -58dB W=3 |
0.42-0.5*cos(2*π*i/(n-1))+0.08*cos(4*π*i/(n-1)), i=0..n-1 |
0.44959-0.49364*cos(2*π*i/(n-1))+0.05677*cos(4*π*i/(n-1)), i=0..n-1 |
|
Cos3 Nutall -64dB W=3 |
0.40897-0.5*cos(2*π*i/(n-1))+0.09103*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman Exact -68dB W=3 |
0.42659071367153912296-0.49656061908856405847*cos(2*π*i/(n-1))+0.076848667239896818573*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman-Harris -68dB W=3 |
0.42323-0.49755*cos(2*π*i/(n-1))+0.07922*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Minimum Sidelobe -71dB W=3 |
0.4243801-0.4973406*cos(2*π*i/(n-1))+0.0782793*cos(4*π*i/(n-1)), i=0..n-1 |
Cos4 Maximum Rolloff -61dB W=4 |
0.3125-0.46875*cos(2*π*i/(n-1))+0.1875*cos(4*π*i/(n-1))-0.03125*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -74dB W=4 |
0.40217-0.49703*cos(2*π*i/(n-1))+0.09892*cos(4*π*i/(n-1))-0.00188*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -83dB W=4 |
0.338946-0.481973*cos(2*π*i/(n-1))+0.161054*cos(4*π*i/(n-1))-0.018027*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -92dB W=4 |
0.35875-0.48829*cos(2*π*i/(n-1))+0.14128*cos(4*π*i/(n-1))-0.01168*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -93dB W=4 |
0.355768-0.487396*cos(2*π*i/(n-1))+0.144232*cos(4*π*i/(n-1))-0.012604*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -96dB W=4 |
0.3635819-0.4891775*cos(2*π*i/(n-1))+0.1365995*cos(4*π*i/(n-1))-0.0106411*cos(6*π*i/(n-1)), i=0..n-1 |
1-1.93*cos(2*π*i/(n-1))+1.29*cos(4*π*i/(n-1))-0.388*cos(6*π*i/(n-1))+0.0322*cos(8*π*i/(n-1)), i=0..n-1 |
Fenêtres d'observation de données de Fourier à largeur variable
Les fenêtres d'observation de données de forme adaptable suivantes sont disponibles dans FlexPro :
Fenêtres |
Calculé en utilisant |
|---|---|
beta |
4*(1-i/(n-1))*i/(n-1))^(-3.218913776512187+2.760793796409310*a), i=0..n-1 a=largeur du lobe principal |
Cosinus maximum Rolloff |
absolute(0.5*(1-cos(2*p*i/(n-1)))))^(a-1), i=0..n-1 Il s'agit de la fenêtre en cosinus avec la décroissance maximale des lobes latéraux. |
Kaiser-Bessel |
I0(sqrt((a²-1.0)/0.10132118361)*sqrt(i*(2*((n-1)/2)-i))/((n-1)/2))/I0(sqrt((a²-1.0)/0.10132118361)), i=0..n-1 a=largeur du lobe principal, I0 est le lobe de Bessel modifié |
van der Maas |
0.5*I1(2*(0.5*π*sqrt(4*a*a-1))*sqrt((i/(n-1))*(1-(i/(n-1)))))/(sqrt((i/(n-1))*(1-(i/(n-1))))*I1(0.5*π*sqrt(4*a*a-1))), i=0..n-1 a=largeur du lobe principal, I1 est le lobe de Bessel modifié |
Cette fenêtre produit le minimum de fuite de lobe latéral, mais offre un rolloff nul. Il est construit dans le domaine fréquentiel et inversé pour produire les données du domaine temporel) FlexPro implémente la fenêtre de Chebychev dans une gamme allant de -30 dB à -150 dB.
Voir le programme 5.2 dans "Programmes IEEE pour le traitement des signaux numériques" |
|
Tchebychev (approximé) |
Il s'agit d'une approximation FlexPro de la fenêtre de Chebshev qui est valable entre -50 et -130 dB. Il est principalement utilisé dans l'objet d'analyse Analyse de Fourier pour données non équidistantes. |
Slepian (DPSS) |
C'est la première des séquences sphéroïdales prolates discrètes de Slepian, ou eigentapers, avec un égal à environ la largeur du lobe principal.
Voir Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis" |
Gaussien |
exp(-4*ln(2)*((i-((n-1)/2))/((n-1)*((2.453274901281656+a*0.3202556336455866)/(1.0+a*(2.348619671799226))))²), i=0..n-1 a=largeur du lobe principal |
Fenêtre d'observation Cosinus |
si(i>(int)(a*n+0,5) et i<(int)((1,0-a)*n-0,5)), 1,0, 0,5-0,5*cos((π/a/(n-1))*(if(i>0,5*n, n-i-1, i)))), i=0..n-1 La fenêtre d'observation va de Hann avec a=0,5 à rectangulaire lorsque a s'approche de 0. |
Les graphiques suivants montrent un certain nombre de fenêtres populaires :
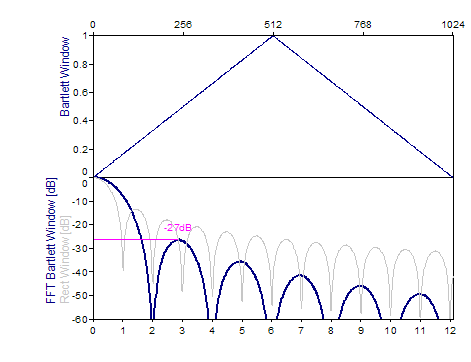
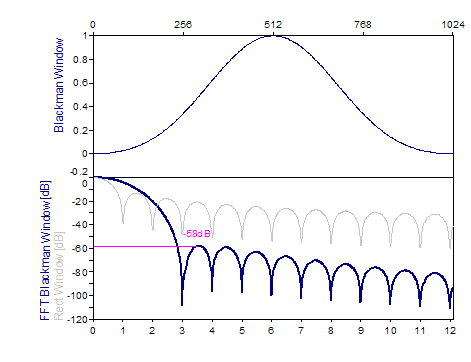
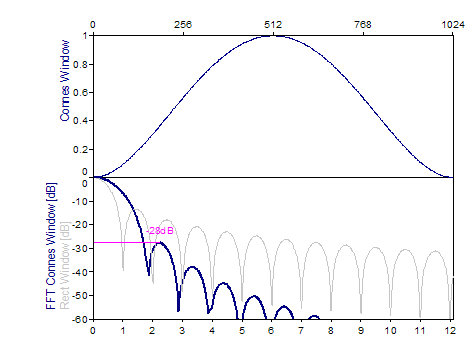
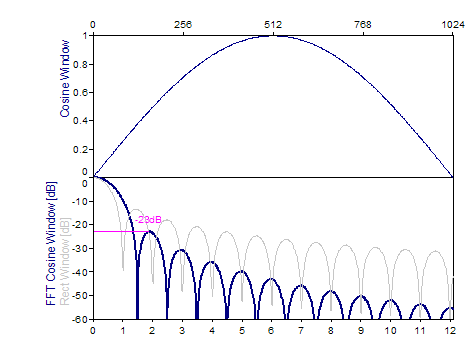
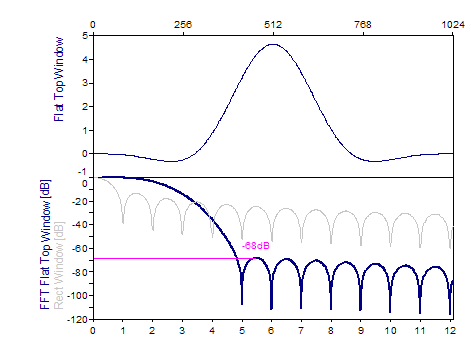
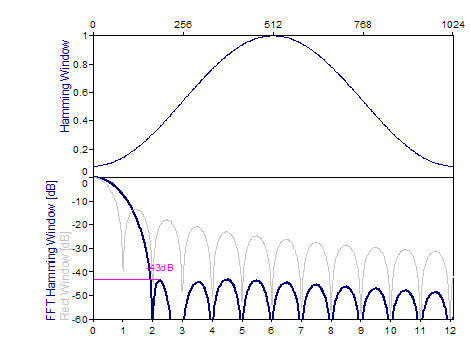
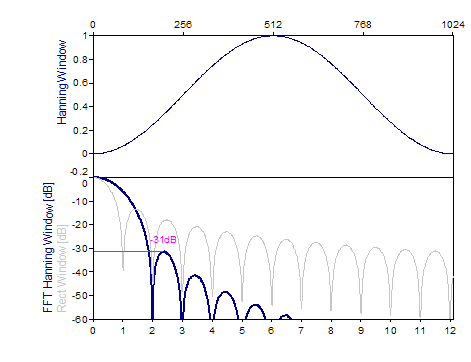
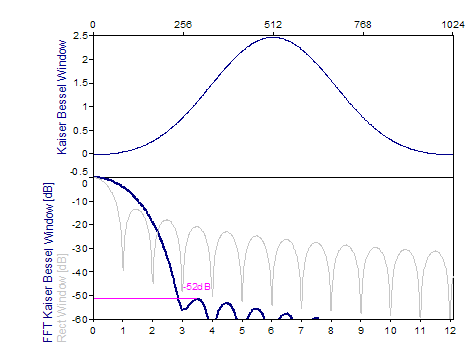
Références
Une implémentation de la fenêtre de Tchebyshev est décrite dans :
•IEEE Programs for Digital Signal Processing, IEEE Press, 1979. FlexPro offre la fenêtre Tchebyshev de -30dB à -150dB.
La fenêtre Slepian (DPSS) est décrite dans :
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.
La référence suivante peut être intéressante :
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.