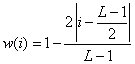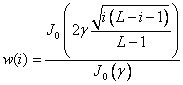Les méthodes de conception des filtres FIR sont basées sur une approximation directe de la réponse en fréquence souhaitée du système à temps discret. Pour cette méthode, les coefficients du filtre correspondent à la réponse impulsionnelle du filtre à concevoir. Pour pouvoir traiter différents signaux, il est nécessaire que ces signaux soient finis. Toutefois, ce n'est pas toujours le cas pour tous les signaux. La méthode de la fenêtre est souvent utilisée pour créer ces types de séquences de signaux finis à partir de séquences infinies. Cette "coupure" d'une séquence infinie pour créer une séquence finie affecte toutefois la plage de fréquences. Cette méthode serait en principe précise, mais comme on ne peut utiliser que plusieurs valeurs finies, ce principe conduit à des déviations qui limitent principalement la pente de la pente et l'atténuation de la bande de coupure réalisables.

L'approximation d'un filtre idéal en coupant la réponse impulsionnelle idéale est identique au problème de convergence dans les séries de Fourier. En raison du comportement des séries de Fourier aux points de discontinuité, une ondulation se produit toujours dans la bande passante et la bande d'arrêt. L'ondulation est intrinsèquement observée si une fonction discontinue est modélisée à l'aide de séries de Fourier. L'ondulation ne disparaît pas non plus lorsque le nombre de coefficients augmente, mais se concentre seulement plus fortement dans la plage de fréquences de coupure. Cet effet est connu sous le nom de phénomène de Gibbs. Une solution peut être trouvée par une pondération appropriée des coefficients du filtre. Les coefficients de frontière sont réduits de manière appropriée. Cependant, l'ordre du filtre nécessaire augmente également pour une pente égale.

Fonctions des fenêtres

Les effets non idéaux, qui sont observés en raison du nombre fini de coefficients de filtre, peuvent être atténués en utilisant une fenêtre de pondération. Le principe est que les coefficients du filtre au milieu sont plus fortement pondérés que les coefficients au début et à la fin.

Il existe plusieurs fonctions de fenêtre qui définissent l'atténuation maximale réalisable de la bande d'arrêt :

Avec cette étape, c'est surtout le comportement d'atténuation qui est amélioré. En contrepartie, la pente est dégradée et le signal subit une atténuation supplémentaire. Par approximation, on peut dire que plus l'atténuation de la bande d'arrêt obtenue augmente, plus la pente est dégradée pour une même longueur de filtre L. Bien sûr, la longueur du filtre peut être augmentée à nouveau afin d'améliorer la pente.

Les fenêtres de Kaiser sont toujours le meilleur choix en ce qui concerne la pente obtenue/la longueur du filtre et l'atténuation de la bande d'arrêt obtenue. En outre, il existe une formule heuristique pour le filtre de Kaiser, qui estime l'ordre du filtre nécessaire à partir des exigences de la bande d'arrêt.

Une description de la fonction de fenêtre de Tchebyshev (fenêtre de Dolph-Tchebyshev) peut être trouvée dans Antoniou, p.440.

Méthode de conception de filtres utilisant la fenêtre de Kaiser

La fenêtre Kaiser remplit une fonction particulière. Le compromis entre la largeur du lobe principal et l'atténuation du lobe latéral peut être quantifié en recherchant une fenêtre concentrée au maximum dans la gamme de fréquences par ω = 0. Kaiser (1966, 1974) a découvert qu'une fenêtre pratiquement optimale peut être trouvée en utilisant une fonction de Bessel modifiée du premier type et d'ordre zéro.

Cette fenêtre peut être ajustée de manière à trouver un compromis entre l'amplitude du lobe latéral et la largeur du lobe principal. Comme pour la fonction de Tchebyshev, la longueur du filtre L peut également être calculée pour la fenêtre de Kaiser à partir des données d'atténuation et de transition. La longueur du filtre est le plus petit nombre impair qui satisfait à l'inéquation suivante, déterminée empiriquement.

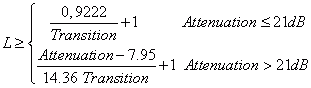
Par exemple, une longueur de filtre d'au moins 17 est nécessaire pour une conception de filtre avec une atténuation de 30 dB dans la bande d'arrêt et une transition de 0,1 (fréquence normalisée).

Algorithme

L'algorithme utilisé dans FlexPro est basé sur le programme FIR1 de L.R. Rabiner, C.A. McGonegal et D. Paul.

Références

•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.

•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.

•L. R. Rabiner, C. A. McGonegal and D. Paul (1979). FIR Windowed Filter Design Program - WINDOW. Section 5.2 dans Programs for Digital Signal Processing, IEEE Press, pp. 5.2-1 to 5.2-19.