Ce tutoriel concerne la conception de filtres FIR et IIR dans FlexPro.

Exemple de signal

À l'aide de l'objet d'analyse Signal, nous allons générer un signal synthétique qui fournira une très bonne démonstration des propriétés du filtre. Sélectionnez Insérer[Données] > Signal > Cosinus wobulé. Configurez la fonction cosinus à fréquence balayée avec la fréquence de 1 et la seconde fréquence de 10000. Dans l'onglet Échantillonnage, déterminez la composante X avec une valeur de départ de 0, une valeur finale de 0,5 et un nombre de valeurs de 1000.

Filtres IIR

Mettez en surbrillance l'ensemble de données Signal.

Cliquez sur Insérer[Analyses] > Assistant d'analyse.

Sélectionnez la catégorie Filtres IIR sous Filtres. Ensuite, sélectionnez Filtre IIR. Cliquez sur Suivant.

L'étape 2 de l'assistant d'analyse contient une boîte de dialogue interactive dans laquelle vous pouvez sélectionner différents types et caractéristiques de filtres. Trois graphiques sont présentés dans la fenêtre d'aperçu de l'assistant d'analyse. Vous pouvez voir le signal d'entrée, la spécification du filtre et le signal filtré ou un graphique avec les coefficients du filtre. Vous pouvez utiliser l'option Afficher la réponse en amplitude pour afficher ou masquer la réponse d'amplitude dans le graphique à l'aide de la spécification du filtre. La réponse en amplitude est également affichée en représentation logarithmique.

Sélectionnez le type de filtre passe-haut et les caractéristiques du filtre de Tchebychev. Ce filtre permet d'influencer l'ondulation dans la bande passante. Activez l'option Utiliser fréquences normalisées. Sélectionnez la spécification du filtre d'ordres 7, la fréquence de coupure normalisée de Fc1 0,25 et la valeur 0,2 comme erreur de bande passante. Notez maintenant que la spécification du filtre généré montre que l'ondulation du filtre se déplace dans la bande passante dans la plage de 0,8 à 1, montrant une erreur maximale de 0,2. Si vous réduisez l'ondulation, la largeur de la transition se déplace au détriment de la raideur du filtre.

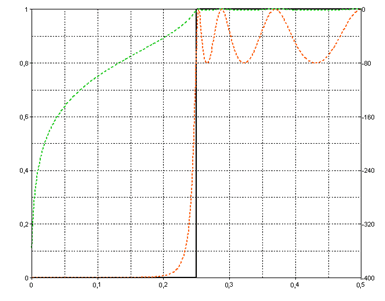
Contrairement au filtre de Tchebyshev, l'ondulation dans la bande d'arrêt est spécifiée pour le filtre de Tchebyshev inverse. La conception du filtre de Cauer est encore plus souple, car il est possible de définir à la fois l'ondulation dans la bande passante et l'ondulation dans la bande d'arrêt.

Un ordre de filtre fixe peut être spécifié pour les filtres IIR. En outre, il est également possible de calculer l'ordre des filtres par rapport à la spécification définie. Au lieu de la fréquence de coupure normalisée, une limite inférieure et supérieure est spécifiée pour une transition. De plus, l'erreur de bande passante et l'erreur de bande d'arrêt sont toutes deux spécifiées. Selon la spécification, le signal filtré ne doit pas dépasser ou descendre en dessous de ces erreurs aux limites de la bande définie.

Sélectionnez Calculer comme ordre, et comme transition, sélectionnez les fréquences normalisées 0,24 et 0,26. Pour chacune des deux erreurs, inscrivez 0,1. Au lieu des erreurs, vous pouvez également spécifier l'ondulation dans la bande passante ou l'atténuation de la bande d'arrêt en décibels. Si vous changez de mode, les valeurs seront converties en conséquence.

Options de résultat Assistant d'analyse

Pour visualiser les objets que l'assistant d'analyse FlexPro peut créer automatiquement, cliquez sur Suivant. À l'étape 3, cochez les deux options actives, puis cliquez sur Terminer.

Sept objets sont créés dans la base de données du projet FlexPro.

FiltreIIR est l'objet d'analyse. Il s'agit de l'objet qui effectue le filtrage. Un double clic sur cet objet ouvre l'objet.

Spécification est la formule permettant de créer la spécification utilisée pour la représentation.

Réponse en amplitude est la formule permettant de créer la réponse en amplitude du filtre, qui est également utilisée pour la représentation.

Le graphique Signal contient le signal d'entrée, le graphique FiltreIIR est la représentation du signal filtré ou des coefficients du filtre, et le graphique Spécification décrit la spécification du filtre.

Le document FiltreIIR contient les trois graphiques générés.

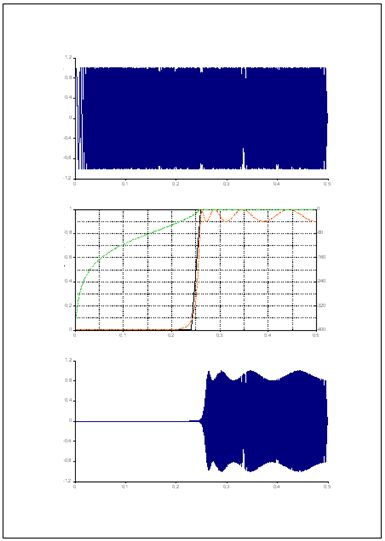
L'ordre du filtre IIR est limité à 10, car des ordres supérieurs peuvent entraîner une instabilité. Par conséquent, examinons maintenant la conception du filtre FIR, qui permet des ordres plus élevés et est également plus flexible que la conception du filtre IIR.

Filtres FIR

Contrairement à la conception du filtre IIR, il existe deux méthodes de calcul différentes pour la conception du filtre FIR : la conception du filtre par fenêtrage et l'algorithme FIR Equiripple (méthode Parks-McClellan).

Conception de filtres FIR par fenêtrage

Nous utiliserons à nouveau le signal synthétique. Mettez en surbrillance l'ensemble de données Signal.

Cliquez sur Insérer[Analyses] > Assistant d'analyse.

Sélectionnez la catégorie Filtres FIR sous Filtres. Ensuite, sélectionnez Méthode de la fenêtre. Cliquez sur Suivant. Sélectionnez Signal filtré comme Résultat et Passe-bande comme Type de filtre. Activez l'option Utiliser fréquences normalisées. Utilisez la fenêtre de Hamming avec les fréquences de coupure Fc1 égale à 0,1 et Fc2 égale à 0,4 et une longueur de filtre de 71. Cliquez sur Terminer. Si vous mettez maintenant en évidence le signal d'entrée et l'objet filtre que vous venez de créer et que vous créez un graphique de lignes, vous remarquerez un déphasage entre les deux signaux. Sur la deuxième page de l'assistant, vous pouvez supprimer ce déphasage en sélectionnant Signal filtré avec correction de phase comme résultat. Pour les filtres FIR, il existe un déphasage constant, qui ne dépend que de la longueur du filtre et de la fréquence d'échantillonnage du signal. La correction de phase est également possible lors de la conception de filtres IIR. Cependant, dans ce cas, la correction de phase se produit lorsque le signal est filtré deux fois : une fois en avant et une fois en arrière.

Maintenant, mettez à nouveau le signal en surbrillance et retournez à l'assistant pour concevoir un filtre en utilisant le fenêtrage. Les différents types de fenêtres présentent un comportement d'atténuation différent. Lorsque l'option Afficher la réponse d'amplitude est activée, à l'exception de la fenêtre de Hamming généralisée, l'atténuation de la bande d'arrêt est dessinée comme une ligne horizontale dans le graphique avec la spécification. L'atténuation est fixée pour les fenêtres Rectangulaire, Bartlett, Hamming, Hanning et Blackman (méthode des fenêtres). Pour la fenêtre de Hamming généralisée, l'atténuation de la bande d'arrêt peut être influencée par le paramètre Alpha, qui peut être compris entre 0 et 1. Les deux fenêtres les plus flexibles sont les fenêtres de Kaiser et de Tchebychev, car ici le troisième paramètre peut être calculé à partir de deux des trois paramètres de longueur de filtre, d'atténuation et de transition.

Sur la deuxième page de l'assistant, sélectionnez Coefficients de filtre pour le résultat. Dans le graphique du bas, la réponse impulsionnelle est maintenant affichée (correspondant aux coefficients du filtre) au lieu du signal filtré. Pour créer une bande passante, sélectionnez la fenêtre de Kaiser avec les fréquences de coupure Fc1 égale à 0,1 et Fc2 égale à 0,4. Sous Calculer, sélectionnez Longueur du filtre. Spécifiez un filtre avec une atténuation de 20 dB et une transition de 0,01. Avec cette méthode, nous obtiendrons une longueur de filtre de 94.

Nous voulons maintenant concevoir un filtre avec les caractéristiques de filtre que nous venons de décrire en utilisant la méthode FIR Equiripple afin de pouvoir comparer les deux méthodes de conception de filtres FIR.

Conception d'un filtre FIR utilisant la méthode Equiripple

Sélectionnez la catégorie Filtres FIR sous Filtres. Ensuite, sélectionnez Méthode Equiripple. Cliquez sur Suivant.

Sélectionnez Coefficients de filtre comme résultat, Passe-bande comme modèle de filtre et calculez la longueur du filtre. Activez l'option Utiliser fréquences normalisées. Dans la liste contenant les bandes, il y a trois bandes prédéfinies pour un passe-bande. La limite supérieure et inférieure de la bande, les facteurs de gain associés et les erreurs d'approximation ou la pondération peuvent être saisis pour chaque bande. La transition entre une bande d'arrêt et une bande passante est formée par la différence entre la limite supérieure d'une bande et la limite inférieure de la bande suivante. Vous pouvez modifier les valeurs individuelles en double-cliquant sur les entrées de la liste. Cependant, pour les modèles de filtres prédéfinis, certaines entrées, telles que les facteurs de gain, ne sont pas accessibles. Ajoutez maintenant les valeurs suivantes à la liste :

Pour ce filtre, une longueur de filtre de 77 est nécessaire lorsqu'on utilise la méthode FIR Equiripple. La bande passante et la bande d'arrêt ont toutes deux une ondulation égale. Ces filtres sont donc appelés filtres Equiripple. Lors de la conception de filtres IIR, une ondulation égale dans la bande passante et la bande d'arrêt est possible en utilisant le filtre de Cauer. Cependant, dans ce cas, l'ondulation ne se déplace pas dans l'intervalle de 1±δ, mais se déplace plutôt entre 1-δ et 1.

Avec la méthode FIR Equiripple, des filtres optimaux peuvent être conçus pour répondre à la spécification. Il en résulte des filtres dont la longueur est inférieure à celle du filtre conçu par fenêtrage. L'autre avantage de la méthode FIR Equiripple est que les filtres multibandes peuvent également être conçus.

Conception d'un filtre multibande

Pour la conception du filtre multibande, nous utiliserons un signal qui contient quatre sinusoïdes de référence de puissance égale sur la plage de Nyquist et trois sinusoïdes de faible puissance placées entre elles. Les composantes de faible puissance seront de -40 dB, -50 dB, et -60 dB en dessous des sinusoïdes de référence. Un bruit blanc sera ensuite ajouté de manière à obtenir un plancher de bruit à environ -75 dB.

Les quatre sinusoïdes de référence et les trois sinusoïdes de puissance inférieure sont définies comme suit :

1.0*sin(2π*x*1005+π/2)+ (0dB)

1.0*sin(2π*x*2005+π/2)+ (0dB)

1.0*sin(2π*x*3005+π/2)+ (0dB)

1.0*sin(2π*x*4005+π/2)+ (0dB)

0.01*sin(2π*x*1505+π/2)+ (-40dB)

0.003162*sin(2π*x*2505+3π/2)+ (-50dB)

0.001*sin(2π*x*3505+π) (-60dB)

Les valeurs x (temps) varient de 0 à 0,1 avec un incrément de 0,0001 échantillon. La fréquence de Nyquist est donc de 5000 (la moitié de la fréquence d'échantillonnage de 10000). Les quatre sinusoïdes de référence couvrent la plage de Nyquist. La première sinusoïde de faible puissance (-40 dB) a 1% de l'amplitude et 0,01% de la puissance de l'une des sinusoïdes de référence. La sinusoïde de faible puissance suivante (-50 dB) a 0,001% de la puissance des références. La dernière des sinusoïdes de test (-60 dB) n'a que 0,1% de l'amplitude et 0,0001% de la puissance des sinusoïdes de référence. Un bruit gaussien à 0,15% a été ajouté pour créer un bruit blanc de fond à environ -75 dB. Ce signal peut également être trouvé dans le tutoriel sur l'analyse spectrale.

Sélectionnez la commande Fichier > Ouvrir Base de données projet et ouvrez la base de données projet C:\Users\Public\Documents\Weisang\FlexPro\2021\Exemples\Filtre.fpd ou C :>Utilisateurs>Public>Documents publics>Weisang>FlexPro2021>Exemples>Filtre.fpd.  Sélectionnez l'ensemble de données Signal2. Cliquez sur Insérer[Analyses] > Assistant d'analyse. Sélectionnez la catégorie Filtres FIR sous Filtres. Ensuite, sélectionnez Méthode Equiripple. Cliquez sur Suivant.

Nous allons maintenant concevoir un filtre multibande qui élimine toutes les composantes du signal, sauf les sinusoïdes à 1000 et 3000 Hz. Pour ce faire, sélectionnez Signal filtré avec correction de phase comme résultat et Multibande comme modèle de filtre. Activez l'option Utiliser fréquences normalisées. Calculez la longueur du filtre. Ajoutez autant de bandes à la liste que nécessaire jusqu'à ce qu'il y ait un total de 5 bandes disponibles. Ajoutez maintenant les valeurs suivantes à la liste :

Vous pouvez maintenant enregistrer ces entrées comme modèle de filtre afin de pouvoir les réutiliser ultérieurement. Pour ce faire, saisissez le nom Multi1 sous Modèle de filtre, puis appuyez sur Enregistrer. Si vous apportez ultérieurement une autre modification à la liste, vous devrez enregistrer à nouveau les entrées. Cliquez sur Terminer. FlexPro enregistre les modèles dans votre profil utilisateur.

Vous pouvez maintenant vérifier le résultat en utilisant une simple FFT. En outre, l'option d'analyse spectrale vous offre encore plus d'options d'analyse, comme la création d'une fonction de transfert à partir du signal d'entrée et du signal filtré.

Conception de filtres utilisant une réponse d'amplitude prédéfinie

À la fin du tutoriel, nous concevrons un filtre en utilisant la méthode FIR Equiripple, où les facteurs de gain ou la réponse en amplitude sont spécifiés comme un ensemble de données. Mettez en surbrillance l'ensemble de données Signal. Rouvrez l'assistant d'analyse et sélectionnez Filtre FIR Méthode Equiripple. Ensuite, définissez les éléments suivants : modèle de filtre personnalisé, calcul de la longueur du filtre, pondération à partir de la liste. Activez l'option Utiliser fréquences normalisées. Définissez les bandes suivantes :

Maintenant, pour le facteur de gain, sélectionnez l'ensemble de données Amplitude. Cet ensemble de données contient une réponse d'amplitude, qui a été générée à partir d'un coupe-bande IIR (filtre Cauer). Si vous jetez maintenant un coup d'œil à la spécification, vous verrez que la spécification du filtre n'est plus définie par des constantes dans la bande d'arrêt et la bande passante, mais qu'elle est plutôt définie par l'ensemble de données spécifié.

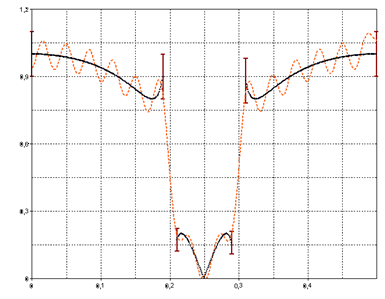
Il est également possible de ne définir qu'une seule bande sur toute la gamme de fréquences de 0 à 0,5. Cependant, il faut s'assurer que les bandes individuelles ne présentent pas de points de discontinuité, sinon l'algorithme ne peut pas converger. En principe, on peut dire que la conception du filtre à l'aide d'une réponse d'amplitude prédéfinie est très gourmande en calculs si la longueur du filtre doit être calculée. De plus, en fonction de la spécification prédéfinie, l'algorithme peut ne pas converger très bien. Dans ce cas, les erreurs d'approximation sont augmentées ou les fréquences de coupure des bandes sont modifiées.

Les pondérations des bandes peuvent également être spécifiées par un ensemble de données si la longueur du filtre est spécifiée comme fixe.

Filtrage de signaux d'entrée multiples

Grâce à l'assistant d'analyse, vous avez également la possibilité de filtrer plusieurs signaux en même temps. Pour ce faire, sélectionnez les signaux à filtrer, ouvrez l'assistant d'analyse et sélectionnez Signal filtré ou Signal filtré avec correction de phase pour le résultat. L'assistant d'analyse génère un objet d'analyse qui calcule les coefficients du filtre. En outre, pour chaque signal d'entrée, une formule FPScript est créée qui filtre le signal d'entrée à l'aide des coefficients de filtre calculés.

Comparaison des filtres IIR/FIR

Dans ce tutoriel, différentes méthodes de conception pour les filtres IIR et FIR ont été présentées. Cela soulève bien sûr la question de savoir quels filtres sont préférables : Filtres IIR ou FIR. Les deux types de filtres présentent des avantages et des inconvénients. Il n'est donc pas possible de répondre à cette question de manière définitive. Vous trouverez ci-dessous une liste de quelques points qui peuvent vous aider à prendre une décision sur le choix à faire :

Filtres IIR

Avantages :

•Calcul simple, car de nombreux filtres sélectifs en fréquence avec des formules de conception fermées peuvent être calculés.

•La spécification de la réponse en amplitude est plus efficace avec les filtres IIR

•Moins de retard de groupe par rapport aux filtres FIR

•Une longueur de filtre plus courte est nécessaire

Inconvénients :

•Pas de phase linéaire

•Retard variable du groupe

•Seulement stable lorsque tous les pôles sont dans le cercle unitaire

Filtres FIR

Avantages :

•Option disponible pour la conception de filtres avec une phase linéaire

•Toujours stables (ne contiennent que des zéros dans la fonction de transition)

•Retard constant du groupe

Inconvénients :

•Méthodes itératives fastidieuses requises

•Plusieurs coefficients sont nécessaires pour obtenir des filtres raides (ordre de filtrage plus élevé par rapport aux filtres IIR)

La méthode FIR Equiripple conduit à des filtres d'ordre inférieur à la méthode de la fenêtre et offre plus d'options pour la mise en forme (pondération, erreurs d'approximation) de la spécification du filtre. En outre, les filtres multibandes peuvent être conçus en utilisant la méthode FIR Equiripple.

Références

Excellentes références d'introduction au filtrage numérique :

•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.

•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.

Les algorithmes de filtrage utilisés dans FlexPro sont décrits dans :

•J.H. McClellan, T.W. Parks, L.R. Rabiner. A Computer Program for Designing Optimum FIR Linear Phase Digital Filters. IEEE Transactions on Audio and Electroacoustics, Vol. AU-21, No.6, December 1973

•L. R. Rabiner, J. H. McClellan and T. W. Parks. FIR Digital Filter Design Techniques Using Chebyshev Approximation. Proceedings IEEE, Vol. 63, No. 4, pp. 595 610, April 1975

•L. R. Rabiner, C. A. McGonegal and D. Paul (1979). FIR Windowed Filter Design Program - WINDOW. Section 5.2 dans Programs for Digital Signal Processing, IEEE Press, pp. 5.2-1 to 5.2-19.

Voir aussi

Option Filtres numériques

Assistant d'analyse

Objet d'analyse Filtre FIR (méthode de la fenêtre)

Objet d'analyse Filtre FIR (méthode Equiripple)

Objet d'analyse Filtre IIR

Méthode de la fenêtre

FIR Méthode Equiripple