Calcule la première dérivée.

Syntaxe

Derivative(Signal [ , Mode = DERIVATIVE_CENTRAL_3_POINTS ])
ou
Derivative(Amplitude, Time [ , Mode = DERIVATIVE_CENTRAL_3_POINTS ])

La syntaxe de la fonction Derivative se compose des éléments suivants :

Remarques

Le résultat est toujours du type de données Virgule flottante de 64 bits.

L'unité du résultat est égale au quotient des unités de Amplitude et Time ou des composantes Y et X de Signal. Pour les matrices de données et les séries de signaux, le calcul s'effectue colonne par colonne. Les valeurs sont converties en points flottants de 64 bits avant que le calcul ne soit effectué. Si elles sont présentes, les composantes X ou Z sont copiées dans le résultat sans modification. La dérivée numérique est calculée en DERIVATIVE_CENTRAL_3_POINTS pour les ensembles de données échantillonnés de manière équidistante (incrément dX) à l'aide des quotients de différence centrale suivants (au moins trois points de données requis) :

Cela correspond à la moyenne des quotients de différence entre le côté gauche et le côté droit (unilatéral), c'est-à-dire :

Dans le mode DERIVATIVE_CENTRAL_5_POINTS la dérivée numérique pour les ensembles de données échantillonnés à équidistance (incrément dX) est calculée à l'aide des quotients de différence centrale suivants (au moins cinq points de données requis) :

Pour les deux variantes, il n'y a pas assez de points d'échantillonnage aux bords pour calculer les différences centrales. La dérivée numérique y est donc calculée à l'aide de quotients de différence finie non centrale du même ordre. Les algorithmes aux bords sont spécifiés dans [1].

Les algorithmes spécifiés de la dérivée numérique peuvent également être généralisés pour les ensembles de données échantillonnés de manière non équidistante ; voir [1]. Ces algorithmes sont également implémentés dans FlexPro et sont utilisés automatiquement dès que l'ensemble de données sous-jacent présente un échantillonnage non équidistant.

Remarque        En général, les dispositions suivantes s'appliquent : Plus l'ordre est élevé lors de la sélection des différences finies, plus la précision de la détermination de la dérivée est grande pour les ensembles de données lisses (non bruyants). Cependant, si les ensembles de données sont bruyants, l'erreur numérique sera pire dans la détermination de la dérivée si une règle de différences finies d'ordre supérieur est utilisée. Le mode de dérivation doit donc être choisi en fonction du bruit/fluidité de l'ensemble de données sous-jacent. Par exemple, le mode DERIVATIVE_CENTRAL_5_POINTS est nécessaire pour les analyses de crashs; voir les directives J1727 de [2] et ECE-R94 de [3].

D'autre part, si l'on s'intéresse au spectre des fréquences, il est utile de considérer les règles dérivées comme des filtres numériques (voir [4]). Les règles dérivées ont la réponse d'amplitude suivante. Le différenciateur idéal est également affiché (profil de filtre de la différenciation continue) ainsi que la différenciation vers l'avant et vers l'arrière à l'aide de la fonction Diff.

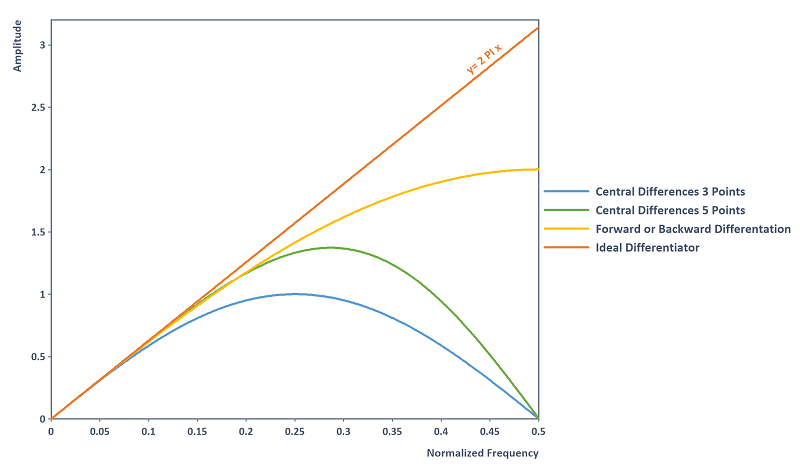
Observation : La règle centrale à 3 points et la règle centrale à 5 points suppriment le bruit haute fréquence dans la limite de Nyquist 0,5. La règle centrale à 5 points présente une approximation plus précise de la réponse d'amplitude du différenciateur idéal sur l'ensemble du domaine fréquentiel que la règle centrale à 3 points. Les quotients de différence unilatérale vers l'avant et vers l'arrière peuvent également avoir une réponse d'amplitude plus précise qui se rapproche du différenciateur idéal, mais amplifient le bruit à haute fréquence en conséquence. Il convient de noter que les règles de différence centrale ont une réponse de phase constante de 90 degrés et correspondent donc précisément à la réponse de phase du différenciateur idéal. D'autre part, les quotients de différence en avant et en arrière ont un déphasage linéaire.

Disponible dans

FlexPro View, Basic, Professional, Developer Suite

Exemples

Derivative(Signal)

Calcule la dérivée discrète d'un signal arbitraire à l'aide de la règle centrale des 3 points.

Derivative({1.0, 3.0, 5.0, 5.0, 4.0, 3.0})

Calcule la dérivée {2, 2, 1, -0,5, -1, -1} de la série de données spécifiée comme argument, où 1,0 est utilisé comme l'incrément dX. Le résultat a la même longueur d'ensemble de données que l'ensemble de données d'entrée.

Diff({1.0, 3.0, 5.0, 5.0, 4.0, 3.0}, DIFF_QUOTIENT_FORWARD)

Calcule les quotients de différence des valeurs voisines à l'aide de la fonction Diff et renvoi {2, 2, 0, -1, -1} comme résultat. La fonction Diff utilise des différences finies non centrales (de premier ordre). La longueur de l'ensemble de données du résultat est donc réduite de un par rapport à l'ensemble de données d'entrée.

Dim x = Series(-6, 6, 0.5)
Derivative(Signal(2.2 + 6.1*x + 3.6*x^2 + 12*x^3 - x^4, x), DERIVATIVE_CENTRAL_5_POINTS)

Calcule la dérivée d'un polynôme du quatrième degré aux points d'échantillonnage x. Le résultat coïncide avec la dérivée exacte Signal(6.1 + 7.2*x + 36*x^2 - 4*x^3, x).

Dim x = Series(-3, 3, 0.1)
Dim f = Signal(Sin(x^2), x)
Dim derivExact = Signal(2*x*Cos(x^2), x)[[ 1.0 ]]
Absolute(Derivative(f, DERIVATIVE_CENTRAL_3_POINTS)[[ 1.0 ]] - derivExact)

Détermine l'erreur pour le mode DERIVATIVE_CENTRAL_3_POINTS lors du calcul de la dérivée numérique de la fonction de lissage f = Sin(x2) au point 1,0. L'erreur est proportionnelle à 0,01. En revanche, si DERIVATIVE_CENTRAL_5_POINTS est sélectionné, cela donne une plus grande précision avec une erreur proportionnelle à 0,0001. Toutefois, si la fonction Diff est utilisée, la dérivée est calculée avec une erreur proportionnelle à 0,1 (précision la plus faible). Pour une approximation de la dérivée, la fonction Derivative devrait donc être utilisée à la place de la fonction Diff.

Voir aussi

Fonction Integral

Fonction SavitzkyGolayDerivative

Fonction Diff

Analyse du signal - Objet d'analyse

Littérature

[1] Bengt Fornberg: Generation of Finite Difference Formulas on Arbitrarily Spaced Grids. Dans: Mathematics of Computation, Vol. 51, No. 184, Pages 699-706. https://doi.org/10.1090/S0025-5718-1988-0935077-0,1988.

[2] Safety Test Instrumentation Stds Comm: Calculation Guidelines for Impact Testing (J1727). Dans: SAE International. http://standards.sae.org/j1727_201502/,2015.

[3] UN Vehicle Regulations: Regulation No. 94 - Frontal collision protection (ECE-R94). Dans: Concerning the Adoption of Uniform Technical Prescriptions for Wheeled Vehicles, Equipment and Parts which can be Fitted and/or be Used on Wheeled Vehicles and the Conditions for Reciprocal Recognition of Approvals Granted on the Basis of these Prescriptions. http://www.unece.org/trans/main/wp29/wp29regs81-100.html,2013.

[4] Tilman Butz: Fourier Transformation for Pedestrians. Springer Berlin Heidelberg New York,http://www.springer.com/de/book/9783319169842,2015.ISBN 3-540-23165-X.