Supprime le décalage CC (DC bias) à l'aide d'un filtre passe-haut numérique (récursif).

Syntaxe

DCRemovalFilter(DataSet, [ CutOffFrequency = 0.01 ], [ SamplingRate ], [ Order = 1 ] [ , PhaseCorrection = True ])
ou
DCRemovalFilter(Result, [ CutOffFrequency = 0.01 ], [ SamplingRate ] [ , Order = 1 ])

La syntaxe de la fonction DCRemovalFilter se compose des éléments suivants :

Remarques

Le filtre correspond à un filtre passe-haut de Butterworth avec l'ordre spécifié Order et la fréquence de coupure CutOffFrequency. On peut aussi créer le filtre passe-haut Butterworth en utilisant la fonction IIRFilter.

Utilisez la première syntaxe pour supprimer le décalage directement des signaux. La structure du résultat correspond à celle de l'argument DataSet. Dans le cas des matrices de données et des séries de signaux, le calcul est effectué sur la base de chaque colonne. Si elles sont présentes, les composantes X ou Z sont copiées dans le résultat sans modification.

Utilisez la deuxième syntaxe pour renvoyer les coefficients du numérateur et du dénominateur du filtre sous la forme d'une liste avec deux éléments b et a, ou les pôles et les zéros du filtre. Les coefficients du numérateur et du dénominateur peuvent être utilisés pour calculer la réponse en amplitude du filtre en utilisant AmplitudeResponse ou la réponse en phase en utilisant PhaseResponse.

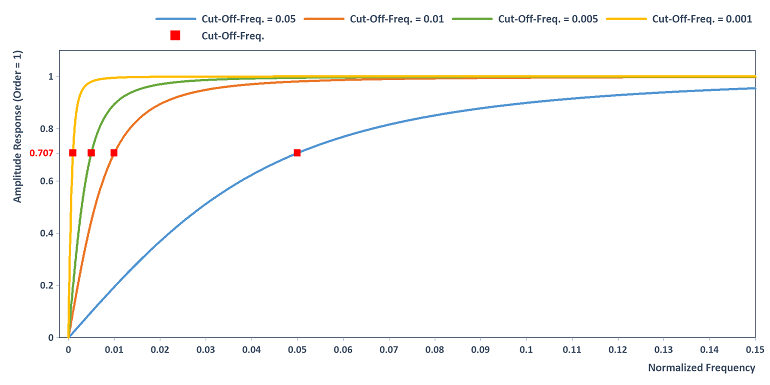
Le filtre a la réponse en amplitude suivante (Order = 1) pour différentes fréquences de coupure. La composante continue est filtrée et les fréquences supérieures à la fréquence de coupure sont transmises presque sans atténuation :

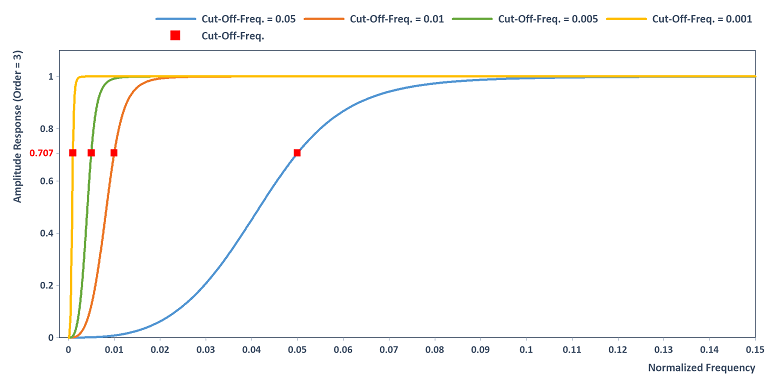
L'augmentation de l'ordre entraîne une augmentation de la pente du filtre passe-haut, par exemple en sélectionnant Order = 3 :

Remarque        Pour le réglage par défaut Order = 1, le filtre est réduit à un filtre récursif commun du premier ordre pour supprimer le décalage DC, également connu sous le nom de Filtre Cascaded-Differentiation-Integration; voir [1, section 13.23] ou [2]. Interprétation de cette dénomination : Le Filtre Cascaded-Differentiation-Integration est formé d'une différenciation en inverse, suivie d'une intégration "fuyante" subséquente avec des constantes de rétroaction . Le différentiateur numérique supprime la composante continue, et l'intégrateur subséquent renvoie le signal d'entrée sans le décalage de la composante continue. Le Filtre Cascaded-Differentiation-Integration (CDI) a la règle de définition récursive suivante :

Le paramètre de l'intervalle [0, 1] peut être calculé uniquement par la fréquence de coupure normalisée ω de l'intervalle [0, 1/4] comme suit :

Disponible dans

FlexPro Basic, Professional, Developer Suite

Exemples

DCRemovalFilter(DataSet)

Supprime la polarisation DC d'un ensemble de données. La fréquence de coupure normalisée est généralement fixée à la fréquence normalisée de 0,01. Cela correspond à une fréquence de coupure d'un centième de la fréquence d'échantillonnage.

DCRemovalFilter(DataSet, 3 Hz, SamplingRate(Signal.X))

Supprime la polarisation DC d'un ensemble de données. La fréquence de coupure est fixée à 3 Hz. Il s'agit d'une fréquence maximale normalisée de 3 Hz / fréquence d'échantillonnage.

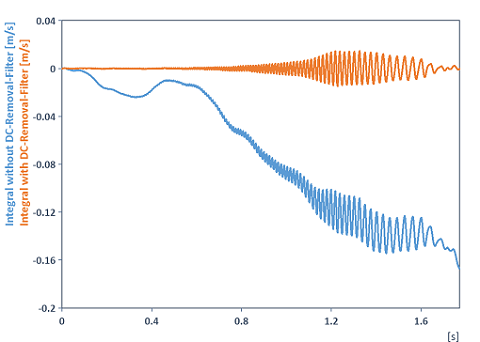
Integral(DCRemovalFilter(Signal))

Intègre un signal et supprime au préalable la dérive ou le décalage (composante continue). Raison : La raison de cette dérive du signal après l'intégration n'est pas seulement l'accumulation de décalage pendant l'intégration, mais aussi la réponse d'amplitude inversement proportionnelle de l'intégrateur (voir fonction Integral). Cela amplifie le bruit à des fréquences proches de l'offset (composante continue) et l'intégration l'élève à des valeurs arbitrairement élevées. La courbe intégrée dérive alors. Pour éviter cette dérive, il ne suffit pas de soustraire la moyenne, mais les fréquences proches de la composante continue doivent également être coupées à l'aide d'un filtre passe-haut. L'illustration suivante clarifie la situation (à titre d'exemple, un des signaux d'accélération des fichiers d'exemple FlexPro sous C:\Users\Public\Documents\Weisang\FlexPro a été intégré) :

Dim coeff = DCRemovalFilter(FILTER_COEFFICIENTSCASCADED, 0.01, , 3)
AmplitudeResponse(coeff, 100000)

Calcule la réponse d'amplitude (avec 100000 points de données) du filtre d'élimination du courant continu pour la fréquence de coupure normalisée de 0,01 et d'ordre 3 à l'aide de la fonction AmplitudeResponse.

Dim coeff = DCRemovalFilter(FILTER_COEFFICIENTSCASCADED, 0.01)
Filter(Signal, coeff, TRUE)

Les coefficients du numérateur et du dénominateur du filtre sont d'abord calculés, puis les données sont filtrées à l'aide de la fonction Filter. Le code est équivalent à : DCRemovalFilter(Signal).

Dim param = DCRemovalFilter(FILTER_POLESANDZEROS, 0.001, , 5)
Signal(Imag(param.Poles), Real(param.Poles))

Calcule les pôles des filtres pour la fréquence de coupure normalisée de 0,001 et d'ordre 5 et les renvoie sous forme de signal. Il convient de noter qu'un ordre trop élevé peut provoquer des artefacts numériques pour des fréquences de coupure trop basses. Les artefacts numériques sont conditionnés mathématiquement par le fait que les pôles du filtre sont sur le cercle unitaire ou s'en approchent très près. Par exemple, pour Order = 1 les pôles sont plus éloignés du cercle unitaire que dans le cas de Order = 5. Le filtre le plus stable numériquement est obtenu pour Order = 1.

Voir aussi

Fonction Detrend

Fonction Integral

Fonction AmplitudeResponse

Fonction PhaseResponse

Fonction IIRFilter

Fonction Filter

Fonction SamplingRate

Option Filtres numériques

Objet d'analyse Filtre IIR

Analyse du signal - Objet d'analyse

Littérature

[1] Richard G. Lyons: Understanding Digital Signal Processing (3rd Edition). Prentice Hall,2011.ISBN 0-13-702741-9.

[2] Richard G. Lyons, Randy Yates: DC Blocker Algorithms. Dans: IEEE Signal Processing Magazine, Vol. 25, Issue 2. 2008.