ACF (FPScript)
Calcule la fonction d'autocorrélation d'un signal. Décrit la similarité d'un signal avec lui-même.
Syntaxe
ACF(Signal [ , Mode = CORRELATIONPRODUCT_NONCIRCULAR ])
La syntaxe de la fonction ACF se compose des éléments suivants :
Section |
Description |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Signal |
L'ensemble de données dont la fonction d'autocorrélation est calculée. Les structures de données autorisées sont Séries de données, Matrice de données, Signal et Série de signaux. Tous les types de données numériques sont autorisés. Les valeurs invalides ne sont pas autorisées dans cet argument. Des restrictions supplémentaires s'appliquent à la composante X.Les valeurs doivent avoir un espacement positif constant. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||||||||||
Mode |
Précise le mode de calcul. L'argument Mode peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut CORRELATIONPRODUCT_NONCIRCULAR . |
Remarques
Le type de données du résultat est toujours Virgule flottante de 64 bits.
La structure du résultat correspond à celle de l'argument Signal.
L'unité du résultat est la même que le carré de l'unité de Signal. L'autocorrélation pour une série de données s est définie comme suit :
![]()
avec le produit de corrélation :
![]()
et N, le nombre de valeurs dans s.
Les valeurs de l'autocorrélation normalisée sont comprises entre -1 et +1. La corrélation normalisée calcule le quotient entre l'autocorrélation et le produit des valeurs RMS des ensembles de données d'entrée.
Le calcul s'effectue dans le domaine fréquentiel dans tous les cas selon la formule suivante :
IRFFTn(*FFTn(Signal) * FFTn(Signal))
Pour les arguments bidimensionnels, le calcul est effectué colonne par colonne, et le résultat est également bidimensionnel. Si l'un des arguments a une composante X, cela s'applique également au résultat.
Pour une autocorrélation circulaire, le calcul se fait en supposant qu'une ou plusieurs périodes complètes du signal sont stockées dans l'ensemble de données. Si le résultat a une composante X, alors cette composante contient le décalage temporel τ de la fonction d'autocorrélation. La valeur τ = 0 est toujours située exactement au début de la série de données X. Par conséquent, aucune valeur τ négative n'est calculée. En raison de la périodicité de l'autocorrélation, les valeurs de la deuxième moitié du résultat peuvent toutefois être considérées comme des valeurs τ négatives dans ce cas.
L'autocorrélation non circulaire est basée sur l'hypothèse que le signal en dehors de la section couverte par l'ensemble de données Signal est égal à zéro. Un nombre suffisant de zéros est donc ajouté à l'ensemble de données avant la transformation dans le domaine des fréquences. La fonction d'autocorrélation est calculée pour toutes les valeurs τ pour lesquelles elle peut avoir une valeur non égale à zéro, c'est-à-dire pour lesquelles il existe encore un chevauchement du signal avec sa copie décalée. Si le résultat a une composante X, alors cette composante contient le décalage temporel τ de la fonction d'autocorrélation. La valeur τ = 0 est toujours exactement au centre de la série de données X.
L'illustration suivante montre différentes variations pour un signal sinusoïdal avec une fréquence de 1, une amplitude de 10 et une plage X de 0 à 10 :
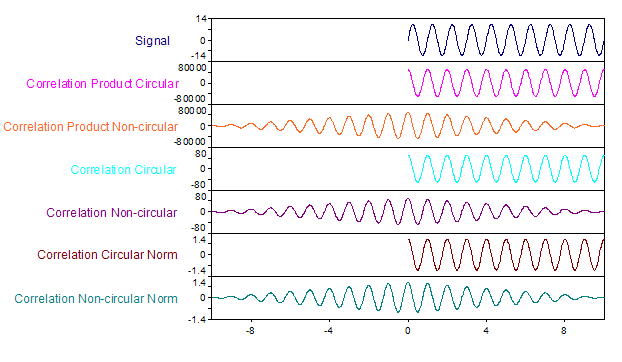
Disponible dans
FlexPro Basic, Professional, Developer Suite
Exemples
ACF(Signal(2. * Sin(2. * PI * 200. * (1000, 0., 1.e-005)) + Noise((1000, 0., 1.e-005), NOISE_NORMAL), (1000, 0., 1.e-005)), CORRELATION_CIRCULAR)
Il existe un signal sinusoïdal de fréquence f = 200 Hz, d'amplitude = 2 V, de phase = 0° et de décalage = 0 V au-dessus de deux périodes. Le signal est superposé à un bruit gaussien (valeur moyenne μ = 0 V, écart-type σ = 1 V).
Grâce à la fonction d'autocorrélation ACF, l'amplitude et la fréquence du signal périodique perturbé sont maintenant récupérées.
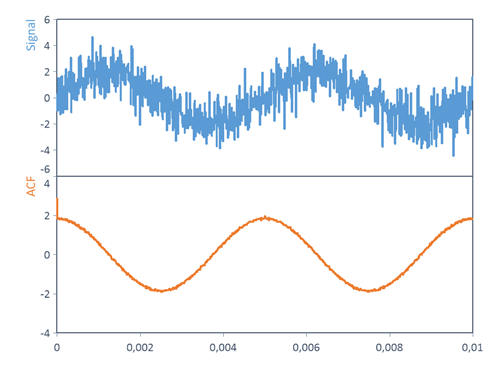
Voir aussi
Littérature
[1] "Oppenheim, A. V. and Schafer, R. W.": "Discrete-Time Signal Processing, 2nd Edition", page 743 - 48. "Prentice Hall, New Jersey",1999.ISBN 0-13-754920-2.
[2] "H.D. Lüke": "Signalübertragung (Signal Transmission)", page 79 - 81. "Springer-Verlag Berlin, Heidelberg, New York",1985.ISBN 3-540-15526-0.
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations