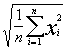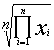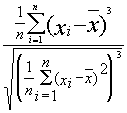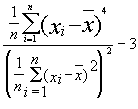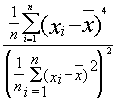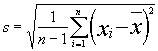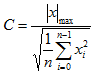weisang.com > Dokumentation > Objet d’analyse Grandeurs Statistiques

Documentation FlexPro

Objet d’analyse Grandeurs Statistiques

09.03.2021

Vous pouvez utiliser cet objet d'analyse pour calculer différentes grandeurs caractéristiques statistiques pour un ensemble de données.

Le calcul d'une grandeur caractéristique statistique conduit d'un échantillon (série de données) à une valeur scalaire, qui décrit une certaine propriété de l'échantillon. Sur la base d'une largeur d'intervalle spécifiée, les valeurs extrêmes, les valeurs moyennes et les quantiles peuvent également être calculés en blocs ou en flottant. Avec le calcul en bloc, le résultat contient une valeur par intervalle. Pour un calcul glissant, le nombre de valeurs reste le même. Pour chaque valeur, on considère la plage autour de cette valeur spécifiée par la largeur de l'intervalle.

Toutes les grandeurs caractéristiques peuvent être déterminées pour toutes les structures de données, à l'exception des valeurs scalaires. Pour les séries de données, le résultat est une valeur scalaire, sauf si un calcul glissant ou en bloc a été sélectionné. Pour les matrices de données, vous pouvez calculer des grandeurs de caractéristiques statistiques soit pour leurs colonnes ou leurs lignes, soit globalement pour l'ensemble des données. Si vous sélectionnez l'option Grandeurs pour colonnes, une grandeur caractéristique est calculée pour chaque colonne individuelle (série de données) dans la matrice de données. Vous obtiendrez alors une série de données dont le nombre de valeurs correspond au nombre de colonnes (séries de données) de la matrice de données. Si vous sélectionnez l'option Grandeurs pour lignes, une grandeur caractéristique est calculée pour chaque ligne. Vous obtenez alors une série de données dont le nombre de valeurs correspond au nombre de lignes de la matrice de données. L'option Moyenner colonnes avant convertit la matrice en une série de données par moyenne arithmétique avant de calculer le paramètre, et l'option Concaténer colonnes avant ajoute les colonnes à une longue série de données. Le résultat correspond alors à celui qui serait obtenu pour une série de données correspondante. Utilisez l'option Concaténer colonnes avant, par exemple, pour déterminer le maximum global d'une série de signaux.

Pour les structures de données agrégées, les signaux, les séries de signaux et les courbes 3D, seule la composante Y est prise en compte. Lors du calcul d'une grandeur caractéristique glissante, les composantes X et Z sont copiées telles quelles dans le résultat. Si une grandeur caractéristique de bloc est calculée, les données des composantes X ou Z, selon la direction du calcul, sont décimées, la première valeur actuelle d'un bloc étant adoptée dans le résultat.

Sommes *

Grandeur Caractéristique	Formule	Note
Somme		Somme des données
Somme carrée		Somme des carrés des données

Valeurs extrêmes

Grandeur Caractéristique	Formule	Note
Minimum		Valeur la plus basse
Maximum		Valeur la plus élevée

Valeurs moyennes

Grandeur Caractéristique	Formule	Note
Moyenne arithmétique		Valeur moyenne
Moyenne quadratique (Valeur effective)		Spécifie l'amplitude d'un signal constant de même puissance.
Moyenne géométrique *		À utiliser lorsque les valeurs mesurées sont des grandeurs relatives (multiplicatives). Correspond à la moyenne arithmétique avec une échelle logarithmique.
Moyenne harmonique *

Moments *

Grandeur Caractéristique	Formule	Note
Skew		Mesure de la symétrie d'une distribution. Les valeurs inférieures ou supérieures à zéro indiquent que la distribution est inclinée vers la gauche ou la droite. L'asymétrie est nulle pour une distribution symétrique.
Excès		L'excès spécifie la différence entre le kurtosis de la fonction considérée et le kurtosis de la fonction de densité d'une grandeur aléatoire normalement distribuée. Les valeurs supérieures ou inférieures à zéro indiquent que le maximum absolu de la distribution est supérieur ou inférieur à celui de la distribution normale attribuée (avec la même variance).
Kurtosis		Le kurtosis est une mesure de la raideur ou du "facteur de pic" d'une distribution.

Grandeur Caractéristique

Formule

Note

Skew

Mesure de la symétrie d'une distribution. Les valeurs inférieures ou supérieures à zéro indiquent que la distribution est inclinée vers la gauche ou la droite.

L'asymétrie est nulle pour une distribution symétrique.

Excès

L'excès spécifie la différence entre le kurtosis de la fonction considérée et le kurtosis de la fonction de densité d'une grandeur aléatoire normalement distribuée. Les valeurs supérieures ou inférieures à zéro indiquent que le maximum absolu de la distribution est supérieur ou inférieur à celui de la distribution normale attribuée (avec la même variance).

Kurtosis

Le kurtosis est une mesure de la raideur ou du "facteur de pic" d'une distribution.

Quantile *

Pour calculer le quantile, les données sont triées par ordre croissant, puis la valeur située à la position n / α est prise. Si n / α n'est pas un nombre entier, l'interpolation se fait entre les deux valeurs voisines.

Grandeur Caractéristique	Formule	Note
Quartile inférieur
Médiane
Quartile supérieur

Mesures de dispersion *

Grandeur Caractéristique	Formule	Note
Plage		Plage entre la valeur la plus élevée et la plus basse.
Écart-type		Racine carrée de la variance.
Variance		Mesure de dispersion carrée, liée à la moyenne arithmétique.
Erreur quadratique moyenne		Comme pour la variance, mais liée au nombre complet de valeurs.
Écart interquartile		Différence entre le quartile supérieur et le quartile inférieur.
Coefficient de variation absolu		Écart-type, lié à la valeur moyenne.
Coefficient de variation relatif		Coefficient de variation, rapporté à son maximum absolu.
Écart absolu moyen par rapport à la médiane
Écart absolu moyen par rapport à la moyenne
Facteur de crête		Valeur de crête, liée à la valeur effective.
Coefficient de dispersion par quartile