Calcule la réponse impulsionnelle d'un filtre en bande FIR à l'aide de l'algorithme Equiripple.

Syntaxe

FIRFilterEquiripple(NumberOfBands, BandEdges, GainFactor, WeightingOfErrors, [ FilterLength ] [ , SamplingRate ])

La syntaxe de la fonction FIRFilterEquiripple se compose des éléments suivants :

Remarques

Les coefficients de filtrage sont renvoyés sous forme de séries de données. Utilisez la fonction Filter pour filtrer les données avec les coefficients de filtrage calculés.

L'argument BandEdges est une matrice de données avec n séries de données, chacune avec deux valeurs à virgule flottante de 64 bits, où n est le nombre de bandes. La première valeur d'une série de données spécifie la limite inférieure de la bande et la deuxième valeur spécifie la limite supérieure de la bande. Les valeurs doivent être en ordre croissant et la largeur de transition entre deux bandes doit être supérieure à 0.

L'argument GainFactor peut être une matrice de données avec n (n = nombre de bandes) séries de données, chacune avec deux valeurs à virgule flottante de 64 bits, ou un signal. 1 définit un passe-bande et 0 un coupe-bande. Si le facteur de gain est une matrice, les valeurs sont affectées aux limites de la bande. La réponse en amplitude des bandes est déterminée à partir de cela. Si un signal est spécifié, n'importe quelle réponse en amplitude peut être fournie. La composante Y contient l'amplitude et les valeurs X contiennent les fréquences associées de 0 à la moitié du taux d'échantillonnage ou de 0 à 0,5. Dans ce cas, toutefois, seules les gammes de fréquences définies dans la liste avec les bandes de fréquences sont utilisées.

L'argument WeightingOfErrors peut être une série de données avec n valeurs à virgule flottante de 64 bits ou un signal. Si la longueur du filtre est spécifiée, il est possible de fournir ici la pondération des erreurs, qui est le rapport entre les limites d'erreur des différentes bandes. Si aucune longueur de filtre n'est spécifiée, alors les limites d'erreur absolues pour les différentes bandes sont spécifiées et la longueur de filtre optimale est déterminée à partir de là. Une pondération plus élevée de la bande de fréquences par rapport à une autre bande de fréquences signifie que la limite d'erreur est plus basse, ce qui signifie qu'il y a moins d'ondulation. Avec une longueur de filtre spécifiée, la pondération peut également être spécifiée comme un signal, où la composante X contient les fréquences 0 à la moitié du taux d'échantillonnage ou 0 à 0,5. Si le facteur de gain et la pondération sont tous deux spécifiés comme un signal, alors les deux signaux doivent contenir les mêmes valeurs X.

Remarque        Une augmentation de l'ordre / de la longueur du filtre fait que le filtre est plus raide et réduit l'ondulation.

Disponible dans

Option Filtres numériques

Exemples

FIRFilterEquiripple(3, {{0, 0.1},{0.12, 0.2},{0.22, 0.5}}, {{0, 0},{1, 1},{0, 0}}, {0.05, 0.01, 0.1})

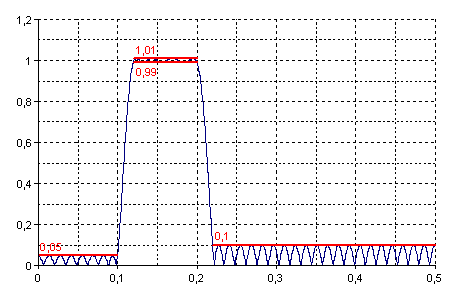
L'illustration suivante montre la réponse en fréquence du filtre FIR multibande calculé. Cela implique trois bandes (bande de coupure, bande passante, bande de coupure) avec des gammes de fréquences de 0 à 0,1, 0,12 à 0,2 et 0,22 à 0,5. L'erreur maximale est de 0,05 pour la première bande, de 0,01 pour la deuxième bande et de 0,1 pour la troisième bande.

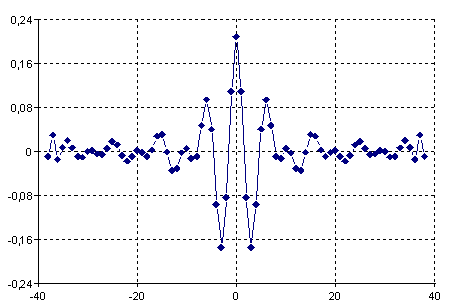
En utilisant la spécification prédéfinie, la fonction détermine un filtre FIR d'une longueur de 77 avec la réponse impulsionnelle suivante :

L'illustration suivante montre un sinusoïde filtrée à l'aide du filtre conçu à cet effet :

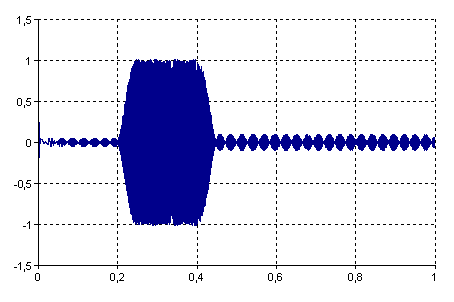
Filter(Signal, FIRFilterEquiripple(3, {{0 Hz, 100 Hz},{120 Hz, 200 Hz},{220 Hz, 500 Hz}}, {{0, 0},{1, 1},{0, 0}}, {0.05, 0.01, 0.1}, , SamplingRate(Signal)), , TRUE)

La fonction filtre un signal avec correction de phase en utilisant le filtre calculé dans le premier exemple. Notez que le deuxième argument de la fonction de filtrage est laissé vide.

Voir aussi

Fonction Filter

Fonction FIRFilterWindow

Fonction IIRFilter

Option Filtres numériques

Objet d'analyse Filtre FIR (méthode Equiripple)

Méthode Equiripple des filtres FIR

Tutoriel sur les filtres