weisang.com > Dokumentation > Distribution (FPScript)

Distribution (FPScript)

21.09.2021

Calcule diverses fonctions de distribution ou de densité.

Syntaxe

Distribution(X, Distribution, Parameter1 [ , Parameter2 ])

 

La syntaxe de la fonction Distribution se compose des éléments suivants :

Section

Description

X

Contient les valeurs X, c'est-à-dire les valeurs de la variable aléatoire pour laquelle la fonction de distribution ou la fonction de densité doit être calculée. Lors du calcul d'une distribution discrète, les valeurs X doivent être intégrales et positives.

Les structures de données autorisées sont Scalaire, Séries de données et Matrice de données. Tous les types de données numériques sont autorisés.

Pour les types de données complexes, un nombre est formé.

Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste.

Distribution

Précise quelle distribution doit être calculée et si la fonction de distribution ou la fonction de densité doit être calculée.

L'argument Distribution peut avoir les valeurs suivantes :

Constante

Signification

DISTRIBUTION_NORMAL

Distribution : distribution normale, Catégorie : continue, Paramètre1 : moyenne, Paramètre2 : variance

DISTRIBUTION_LOGNORMAL

Distribution : distribution normale logarithmique, Catégorie : continue, Paramètre1 : moyenne, Paramètre2 : variance

DISTRIBUTION_EXPONENTIAL

Distribution : distribution exponentielle, Catégorie : continue, Paramètre1 : lambda

DISTRIBUTION_WEIBULL

Distribution : Distribution de Weibull, Catégorie : continue, Paramètre1 : alpha, Paramètre2 : bêta

DISTRIBUTION_CHISQUARE

Distribution : distribution chi carré, Catégorie : test, Paramètre1 : n

DISTRIBUTION_T

Répartition : distribution de Student-t, Catégorie : test, Paramètre1 : n

DISTRIBUTION_F

Distribution : Distribution F, Catégorie : test, Paramètre1 : m, Paramètre2 : n

DISTRIBUTION_BINOMIAL

Distribution : distribution binomiale, Catégorie : discrète, Paramètre1 : n, Paramètre2 : p

DISTRIBUTION_POISSON

Distribution : Distribution de Poisson, Catégorie : discret, Paramètre1 : Lambda

+ DISTRIBUTION_DENSITY

Si la fonction de densité doit être calculée, alors la valeur DISTRIBUTION_DENSITY doit être ajouté. Sinon, la fonction de distribution est calculée. Seules les fonctions de densité peuvent être calculées pour les distributions de test.

Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété.

Parameter1

Spécifie le premier paramètre de la distribution à calculer.

Les structures de données autorisées sont Scalaire. Tous les types de données numériques sont autorisés.

Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété.

Parameter2

Si nécessaire, précise le deuxième paramètre de la distribution à calculer.

Les structures de données autorisées sont Scalaire. Tous les types de données numériques sont autorisés.

Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété.

Remarques

Le résultat est toujours du type de données Virgule flottante de 64 bits.

Les distributions sont calculées sur la base de diverses formules d'approximation. Avant d'utiliser les distributions calculées avec cette fonction à des fins statistiques, vous devez vérifier si la précision est suffisante pour votre tâche.

Disponible dans

Option Statistiques avancées

Exemples

Dim x = (100, -5, 0.101010101010101)
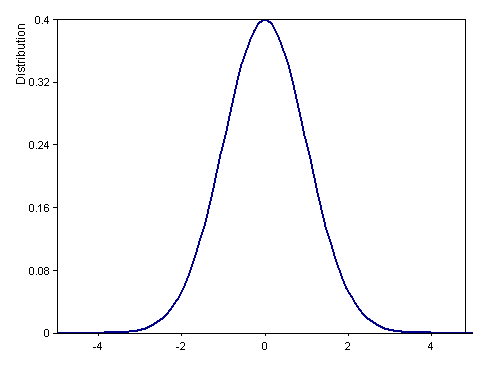
Signal(Distribution(x, DISTRIBUTION_NORMAL + DISTRIBUTION_DENSITY, 0, 1), x)
 

Calcule la fonction de densité de la distribution normale standard (moyenne 0, variance 1) dans l'intervalle [-5, 5].

Voir aussi

Objet d'analyse Distribution

Option Statistiques avancées

Littérature

[1] "Hartung, Joachim": "Statistik (Statistics), 9th Edition". "Oldenbourg Verlag GmbH, Munich",1993.ISBN 3-486-22055-1.

Partager l’article ou envoyer par mail :

Vous serez probablement intéressé par les articles suivants :