Objet d’analyse Convolution *
Vous pouvez utiliser cet objet d'analyse pour calculer le produit de convolution de deux ensembles de données.
Pour le produit de convolution circulaire, le calcul se fait en supposant qu'une ou plusieurs périodes complètes d'un signal périodique sont enregistrées dans les deux ensembles de données. Pour ces variations, les deux ensembles de données doivent avoir le même nombre de valeurs. Le résultat a donc également ce nombre de valeurs. Si l'un des arguments a une composante X, cela s'applique également au résultat. Cette composante contient alors le décalage temporel τ de la convolution.
Le produit de convolution non circulaire est basé sur l'hypothèse que les signaux situés à l'extérieur de la section spécifiée par les ensembles de données sont égaux à zéro. Un nombre suffisant de zéros est donc ajouté aux deux ensembles de données avant le passage au domaine fréquentiel. Si l'un des arguments a une composante X, cela s'applique également au résultat. Cette composante contient alors le décalage temporel τ de la convolution. Le produit de convolution est calculé pour toutes les valeurs de τ pour lesquelles la convolution peut avoir une valeur non égale à zéro, c'est-à-dire pour lesquelles il existe encore un chevauchement des deux signaux.
L'illustration suivante montre une application de l'intégrale de convolution. Il s'agit d'un filtre passe-bas dans le domaine temporel. Le signal est convolué avec la réponse impulsionnelle d'un filtre passe-bas :
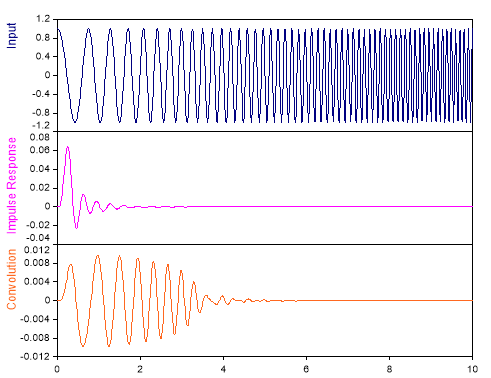
Fonctions FPScript utilisées
Voir aussi
* Cet objet d'analyse n'est pas disponible dans FlexPro View.