CompensatingSpline2D (FPScript)
Interpole un ensemble de données bidimensionnelles à travers une grille de courbes splines de compensation et échantillonne ces courbes à des points définissables.
Syntaxe
CompensatingSpline2D(Surface, NX, NZ, SamplingMode, Weighting)
ou
CompensatingSpline2D(DataMatrix, LocusX, LocusZ, NX, NZ, SamplingMode, Weighting)
La syntaxe de la fonction CompensatingSpline2D se compose des éléments suivants :
Section |
Description |
||||||
|---|---|---|---|---|---|---|---|
Surface |
La matrice de données ou série de signaux avec une composante Z et un intervalle d'échantillonnage constant, qui est interpolée. Si les composantes X et Z sont manquantes, elles seront générées automatiquement. Les structures de données autorisées sont Matrice de données et Série de signaux. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors la fonction est exécutée pour chaque élément de la liste et le résultat est également une liste. |
||||||
DataMatrix |
Matrice de données avec la composante Y de la série de signaux à interpoler. Si vous spécifiez une série de signaux, alors sa composante Y est utilisée. Les structures de données autorisées sont Matrice de données et Série de signaux. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
LocusX |
Séries de données avec la composante X de la série de signaux à interpoler. Si vous spécifiez un signal, alors sa composante Y est utilisée. Les structures de données autorisées sont Séries de données et Signal. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
LocusZ |
Séries de données avec la composante Z de la série de signaux à interpoler. Si vous spécifiez un signal, alors sa composante Y est utilisée. Les structures de données autorisées sont Séries de données et Signal. Tous les types de données numériques sont autorisés. Pour les types de données complexes, un nombre est formé. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
NX |
Spécifie le nombre total de points ou par intervalle X de la série de signaux. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
NZ |
Spécifie le nombre total de points ou par intervalle Z de la série de signaux. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
SamplingMode |
Spécifie comment la surface spline calculée doit être échantillonnée. L'argument SamplingMode peut avoir les valeurs suivantes :
Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
||||||
Weighting |
Précise la mesure de compensation pour la surface de la spline. Les valeurs proches de zéro donnent une ligne droite, et les valeurs très élevées donnent une surface spline naturelle. Les structures de données autorisées sont Scalaire. Tous les types de données réels sont autorisés. La valeur doit être supérieure ou égale à 0. Si l'argument est une liste, alors son premier élément est pris. S'il s'agit à nouveau d'une liste, le processus est répété. |
Remarques
Le résultat est toujours du type de données Virgule flottante de 64 bits.
Le résultat a la même unité que l'argument Surface.
Tout d'abord, pour chaque ligne de la grille donnée par la composante Y de l'ensemble de données, une courbe spline de compensation est modélisée et évaluée aux positions Z souhaitées. Ce type de courbe spline est constitué de polynômes cubiques, qui sont ajoutés les uns aux autres pour obtenir la variation le plus lisse possible. Ensuite, pour chaque colonne de la matrice de données ainsi calculée, une courbe spline est modélisée et évaluée aux positions X souhaitées. Dans la fonction spline d'approximation, les polynômes ne passent pas nécessairement par les points de l'ensemble de données, mais ils les équilibrent. La mesure de compensation peut être modifiée par la surface spline naturelle, qui passe par les points, jusqu'au plan le mieux approximé. Avant chaque interpolation spline, les valeurs invalides (void) dans les lignes ou les colonnes sont éliminées par interpolation linéaire. La composante Y de l'ensemble de données à interpoler doit contenir au moins 3 x 3 valeurs, et les composantes X et Z doivent être strictement croissantes.
Les illustrations suivantes montrent deux surfaces splines 2D de compensation avec des pondérations différentes et les données sur lesquelles elles sont basées :
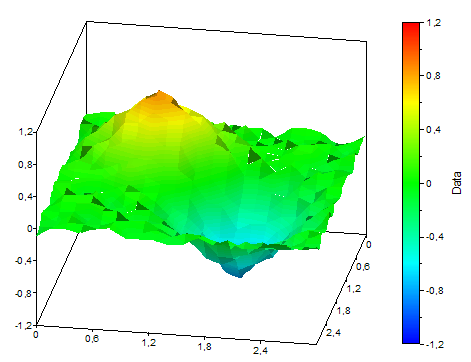
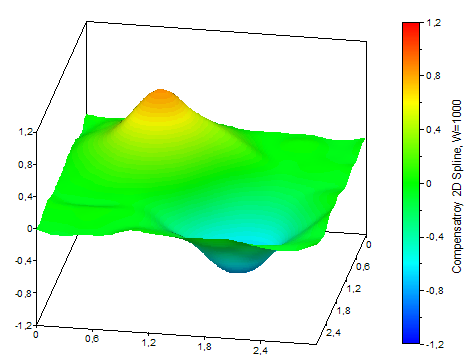
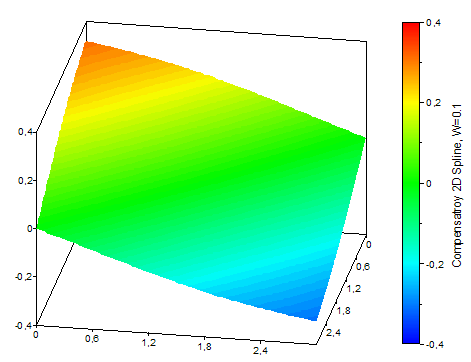
Disponible dans
FlexPro Basic, Professional, Developer Suite
Exemples
CompensatingSpline2D({{0, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, -1, 0}, {0, 0, 0, 0}}, 100, 100, SPLINE_EQUIDISTANT, 1000) |
Interpole la matrice de données à travers une grille de courbes splines compensatrices avec une pondération élevée. |
Voir aussi
Objet d'analyse Interpolation Spline
Objet d'analyse Interpolation de surface
Objet d'analyse Approximation 2D
Littérature
[1] "Carl de Boor": "A Practical Guide to Splines, Revised Edition". "Springer-Verlag, New York",2001.ISBN 0-387-95366-3.