Algorithme SavitzkyGolay
Les filtres passe-bas, qui filtrent les hautes fréquences, sont souvent utilisés pour lisser les données. Les oscillations à haute fréquence - notamment les erreurs de mesure - sont ainsi réduites au minimum.
Contrairement à la plupart des filtres passe-bas utilisés dans le domaine de Fourier, le filtre Savitzky-Golay est utilisé dans le domaine temporel. Imaginez le filtre comme une fenêtre qui se déplace sur les données et attribue une valeur moyenne à chaque point de données dans la fenêtre associée (moyenne de la fenêtre glissante) :
![]()
gi est la valeur filtrée à la position i.
fj est la valeur non filtrée à la position j.
nL spécifie les points de données à gauche du point à lisser.
nR spécifie les points de données à droite du point à lisser.
cn est la fonction de pondération.
La méthode du filtre SavitzkyGolay effectue une régression polynomiale locale afin de déterminer les valeurs lissées pour chaque point de données. Cette méthode est supérieure à celle de la moyenne glissante, car elle conserve les attributs des données tels que l'amplitude et la longueur des impulsions, qui sont généralement dégradés par la moyenne glissante. Cette méthode est particulièrement utilisée lorsqu'un pic n'a été échantillonné que par quelques points. La position et la hauteur du pic peuvent être estimées, même si le maximum se situe entre deux points de prélèvement.
Les coefficients cn sont choisis de manière à ce que les moments supérieurs soient préservés. Contrairement à la moyenne glissante, les coefficients ne sont pas calculés par une constante (estimée par la valeur moyenne), mais sont fournis par un polynôme d'ordre supérieur. Une estimation par la méthode des moindres carrés est utilisée pour le calcul. Heureusement, il n'est pas nécessaire de recalculer les coefficients pour chaque point. Le calcul est en fait indépendant des données réelles et ne dépend que du degré du polynôme. L'ajustement est effectué par une estimation des moindres carrés (estimation LS) entre la matrice A et le vecteur f :
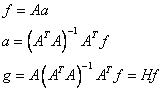
H est également appelée la matrice "chapeau" et est la même pour chaque f pour un polynôme donné. Il peut également effectuer le calcul une fois et l'enregistrer pour une utilisation ultérieure. Pour calculer les coefficients, une seule ligne de la matrice inverse doit être calculée. On peut l'obtenir, par exemple, à partir de la décomposition LU en utilisant une seule substitution arrière.
Remarque : La méthode de lissage Savitzky-Golay est également appelée filtre polynomial de lissage numérique (DISPO).
Références
•Savitzky A., and Golay, M.J.E. (1964). Analytical Chemistry, vol. 36, p. 1627–1639.
•W. H. Press, et. al. (1992). Numerical Recipes in C, Second Edition. Cambridge University Press, p. 650-655.
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations