Objet d’analyse Transformation en Rosette *
Avec cet objet d'analyse, vous pouvez utiliser une rosette de jauges de contrainte pour calculer diverses quantités, telles que les contraintes principales ou les déformations principales.
Une rosette de jauges de contrainte est un réseau de deux ou plusieurs grilles de jauges de contrainte étroitement espacées et d'orientations différentes pour mesurer les contraintes normales sur la surface sous-jacente d'un objet à tester. Dans le cas d'un état de contrainte biaxiale dont les directions principales sont inconnues, trois mesures de déformation indépendantes dans des directions différentes sont suffisantes pour déterminer les déformations et les contraintes principales.
Propriétés de Rosette
Le calcul pour les types de rosettes suivants est possible :
Description |
Description |
|---|---|
Rosette T |
Deux grilles perpendiculaires ; position a et b |
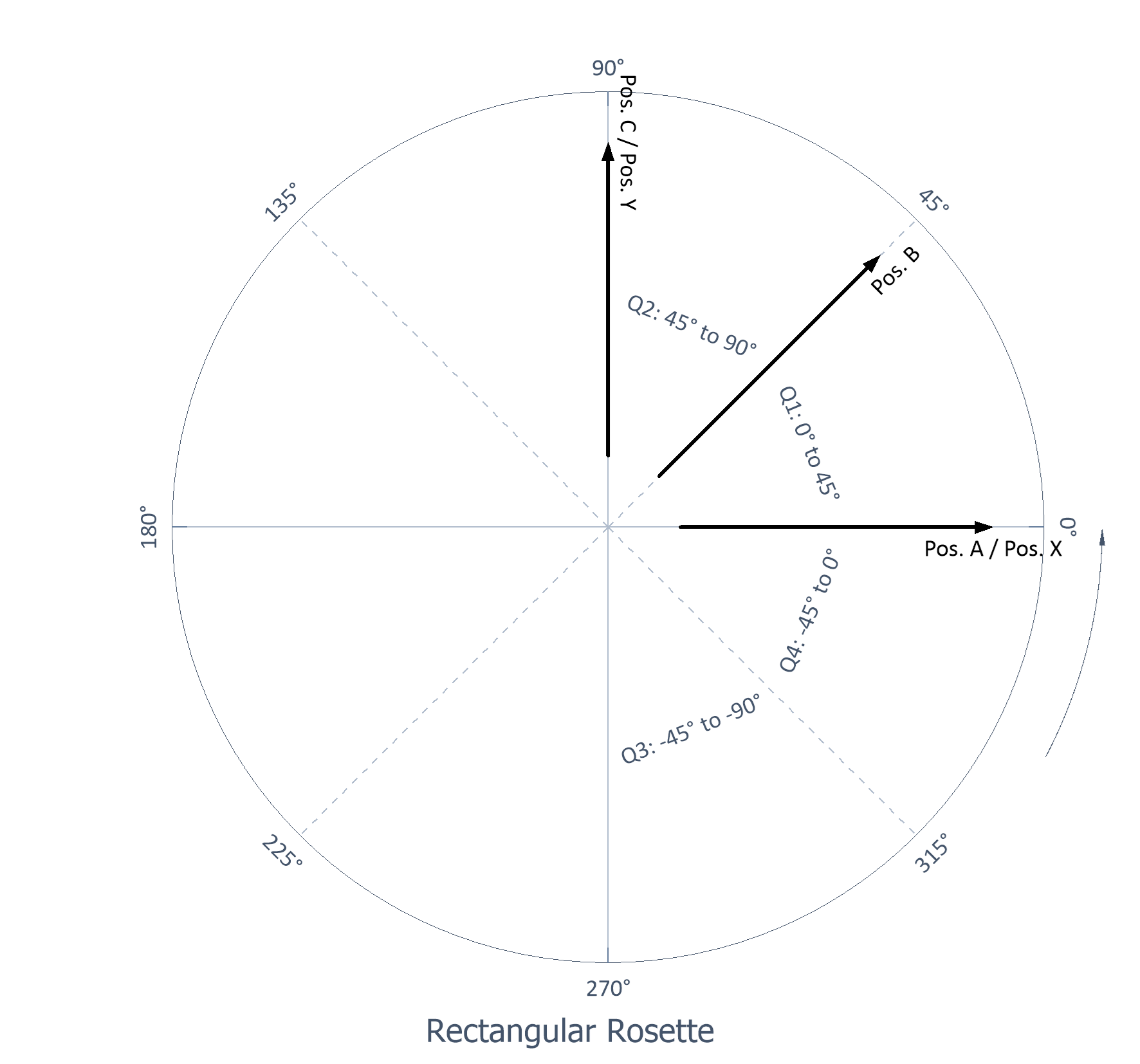
Rosette rectangulaire |
Trois grilles, avec 45° entre les grilles |
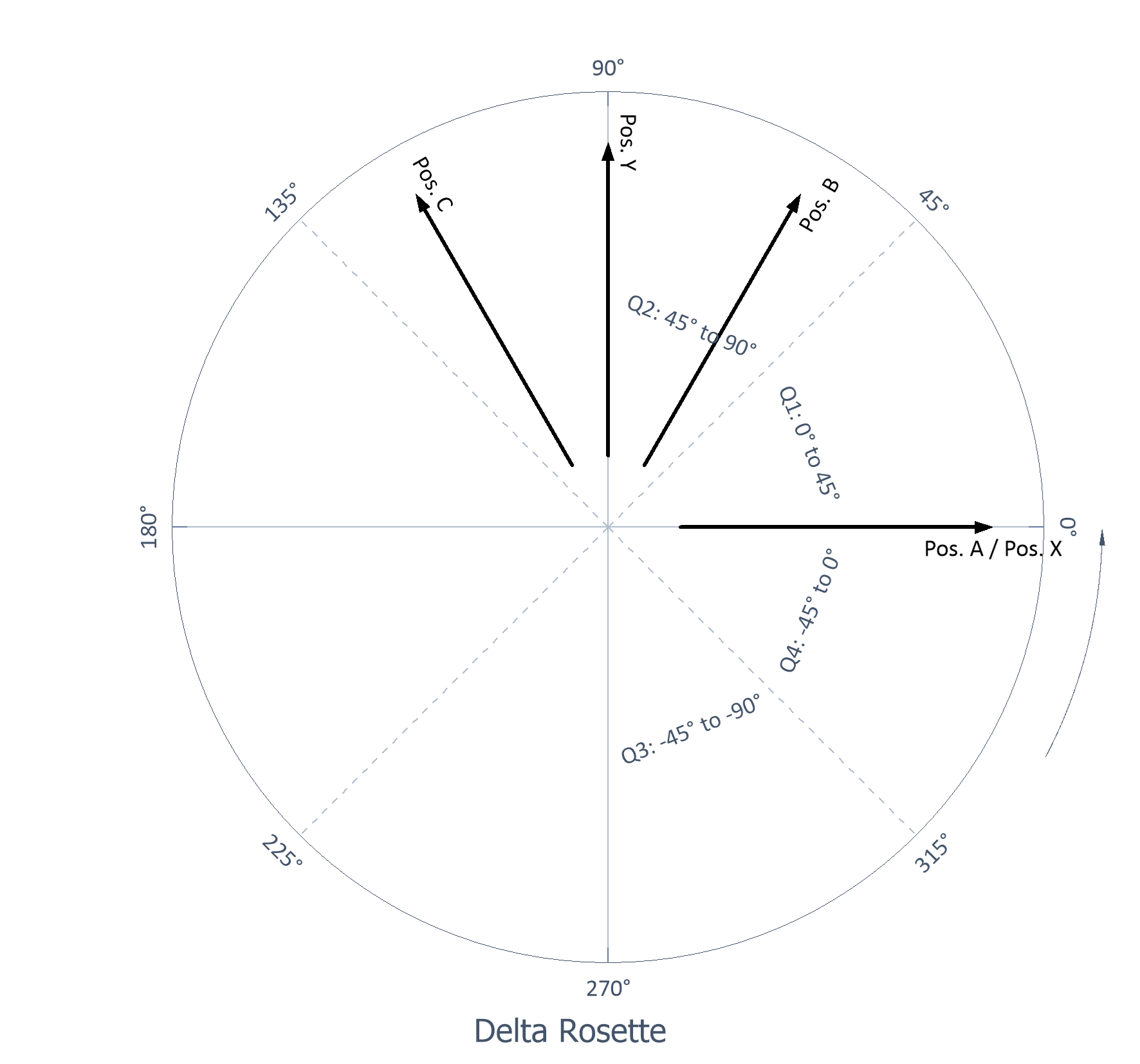
Rosette delta |
Trois grilles, les deuxième et troisième grilles étant espacées de 60° et 120° |
Si le matériau de l'objet testé est de composition homogène, se comporte de manière isotrope et présente une relation contrainte-déformation linéaire, la loi de Hook pour l'état de contrainte biaxiale peut être appliquée pour calculer les contraintes principales à partir des déformations principales. Il est nécessaire de connaître le module d'élasticité E (module de Young) et le coefficient de Poisson du matériau à mesurer [1, 2].
Sensibilité transversale
Le terme sensibilité transversale, ou sensibilité aux déformations transversales, fait référence à la réponse des jauges de contrainte lorsque des déformations leur sont appliquées transversalement à l'axe longitudinal de la grille. Idéalement, il est souhaitable que les jauges de contrainte soient totalement insensibles à ces déformations transversales. En pratique, cependant, la plupart des jauges de contrainte sont sensibles à la contrainte transversale dans une certaine mesure. Heureusement, la sensibilité transversale des jauges de contrainte à film modernes est très faible, de l'ordre de quelques points de pourcentage de la sensibilité de la contrainte dans la direction de la grille. L'ampleur de la sensibilité à la déformation transversale dépend de l'alliage et de la géométrie de la grille.
Une correction mathématique peut être effectuée en spécifiant la sensibilité transversale [3]. Avec l'objet d'analyse, les signaux de déformation corrigés peuvent être émis et ainsi comparés aux signaux de déformation mesurés.
Compensation de température
En option, une compensation de température peut être effectuée pour les signaux de déformation mesurés. On suppose ici que les jauges de déformation sont autocompensées, c'est-à-dire que l'influence de la résistance du câble a déjà été éliminée. L'influence de la température sur le ruban de connexion des jauges de contrainte n'est pas non plus prise en compte. L'erreur résiduelle est déterminée par une fonction polynomiale spécifiée dans la fiche technique de la jauge de contrainte. En plus de la fonction polynomiale, la formule utilisée comprend des termes pour la dépendance à la température du facteur de jauge et la prise en compte supplémentaire d'un écart entre le coefficient de dilatation thermique du matériau sur lequel la mesure a été effectuée et le coefficient de dilatation thermique du matériau de la grille de jauge de contrainte [4, 5].
Les coefficients polynomiaux sont spécifiés comme une série de données. La première valeur correspond au coefficient a0, la deuxième valeur correspond au coefficient a1, etc.
La formule suivante est utilisée pour la compensation de la température :
Description |
Symbole |
|
|---|---|---|
Ensemble de données de déformations |
εu(T) |
|
Ensemble de données de température |
T |
|
Coefficients polynomiaux |
a0, a1, a2, ... |
|
Température de référence |
TRef |
|
Facteur de jauge |
kD |
|
Coefficient de dilatation du matériau |
αM |
|
Coefficient de température du facteur de jauge |
αk |
|
Coefficient de dilatation de la jauge de contrainte |
αSG |
Options de résultat
Les options de résultat suivantes sont disponibles :
Désignation |
Description |
|
|---|---|---|
Déformation principale 1 |
Déformation principale 1 |
|
Déformation principale 2 |
Déformation principale 2 |
|
Contrainte principale 1 |
Contrainte dans la direction de la déformation principale 1 |
|
Contrainte principale 2 |
Contrainte dans la direction de la déformation principale 2 |
|
Angle |
Angle |
|
Déformation de cisaillement |
Déformation de cisaillement |
|
Contrainte de cisaillement |
Contrainte dans le sens de la déformation de cisaillement |
|
Contrainte de von Mises équivalente |
Contrainte de von Mises équivalente |
|
Déformation X |
Correspond à la déformation corrigée à la position a. |
|
Déformation Y |
Correspond à la déformation déplacée de 90° dans le sens inverse des aiguilles d'une montre à la position a. |
|
Contrainte X |
Contrainte dans le sens de la déformation X |
|
Contrainte Y |
Contrainte dans le sens de la déformation Y |
|
Déformation corrigée à la position a |
Déformation corrigée à la position a à l'aide de la sensibilité transversale |
|
Déformation corrigée à la position b |
Déformation à la position b corrigée à l'aide de la sensibilité transversale |
|
Déformation corrigée à la position c |
Déformation à la position c corrigée à l'aide de la sensibilité transversale |
Formules de calcul
Rosette T :
Désignation |
Formule |
|
|---|---|---|
Déformation principale 1 |
||
Déformation principale 2 |
||
Contrainte principale 1 |
||
Contrainte principale 2 |
||
Angle |
90° |
|
Déformation de cisaillement |
0 |
|
Contrainte de cisaillement |
||
Contrainte de von Mises équivalente |
||
Déformation X |
Correspond à la déformation principale 1 |
|
Déformation Y |
Correspond à la déformation principale 2 |
|
Contrainte X |
Correspond à la contrainte principale 1 |
|
Contrainte Y |
Correspond à la contrainte principale 2 |
|
Déformation corrigée en position a, position b |
Rosette rectangulaire :
Désignation |
Formule |
|
|---|---|---|
Déformation principale 1 |
||
Déformation principale 2 |
||
Contrainte principale 1 |
||
Contrainte principale 2 |
||
Angle |
||
Déformation de cisaillement |
||
Contrainte de cisaillement |
||
Contrainte de von Mises équivalente |
||
Déformation X |
||
Déformation Y |
||
Contrainte X |
||
Contrainte Y |
||
Déformation corrigée en position a, position b |
Rosette Delta :
Désignation |
Formule |
|
|---|---|---|
Déformation principale 1 |
||
Déformation principale 2 |
||
Contrainte principale 1 |
||
Contrainte principale 2 |
||
Angle |
||
Déformation de cisaillement |
||
Contrainte de cisaillement |
||
Contrainte de von Mises équivalente |
||
Déformation X |
||
Déformation Y |
||
Contrainte X |
||
Contrainte Y |
||
Déformation corrigée en position a, position b |
avec
Références
[1] Micro-Measurements. Tech Note TN-515: Strain Gage Rosettes: Selection, Application and Data Reduction.Numéro de document : 11065, Révision 14-Août-2014.
[2] Karl Hoffmann. An Introduction to Stress Analysis using Strain Gauges. www.hbm.com
[3] Micro-Measurements. Tech Note TN-509: Errors Due to Transverse Sensitivity in Strain Gages.Numéro de document : 11059, Révision 28-Jun-2011.
[4] Hottinger Baldwin Messtechnik GmbH. Technical Information T05414_01_E00_01: Temperature compensation of strain gauge ¼-bridges – Clear, brief and understandable
[5] Micro-Measurements. Tech Note TN-504-1: Strain Gage Thermal Output and Gage Factor Variation with Temperature.Numéro de document : 11054, Révision 14-Août-2014.
Fonctions FPScript utilisées
StrainGaugeTemperatureCompensation
* Cet objet d'analyse n'est pas disponible dans FlexPro View et FlexPro Basic.
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations