MinimumCircumscribedCircle (FPScript)
Calcule le cercle circonscrit minimum (MCCI) d'un ensemble de points bidimensionnels. Utilisé pour déterminer la rondeur.
Syntaxe
MinimumCircumscribedCircle(Points, [ OutputOptions = MCCI_OUTPUT_CIRCUMSCRIBED_CIRCLE ], [ CircleSize = 5000 ] [ , ConvexHullAlgorithm = CONVEXHULL_GRAHAM_SCAN ])
ou
MinimumCircumscribedCircle(Y, X, [ OutputOptions = MCCI_OUTPUT_CIRCUMSCRIBED_CIRCLE ], [ CircleSize = 5000 ] [ , ConvexHullAlgorithm = CONVEXHULL_GRAHAM_SCAN ])
La syntaxe de la fonction MinimumCircumscribedCircle se compose des éléments suivants :
Section |
Description |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Points |
Le point Y et X fixé pour lequel le cercle circonscrit minimum doit être calculé. La même unité doit être utilisée pour les deux composantes du signal. Les structures de données autorisées sont Signal. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. |
||||||||||||||||||||||
Y |
Les points Y utilisés pour calculer le cercle circonscrit minimum. Si vous spécifiez un signal, sa composante Y est utilisée. L'unité doit correspondre à l'unité de l'argument X. Les structures de données autorisées sont Séries de données et Signal. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. |
||||||||||||||||||||||
X |
Les points X utilisés pour calculer le cercle circonscrit minimum. Si vous spécifiez un signal, sa composante Y est utilisée. L'unité doit correspondre à l'unité de l'argument Y. Les structures de données autorisées sont Séries de données et Signal. Tous les types de données réels sont autorisés, sauf Temps calendaire et Période de temps. |
||||||||||||||||||||||
OutputOptions |
Précise les résultats qui doivent être renvoyés. Les résultats multiples sont présentés sous forme de liste. Si, par exemple, le rayon du cercle de référence et la circularité doivent être indiqués, l'argument doit contenir la valeur MCCI_OUTPUT_CIRCUMSCRIBED_CIRCLE_RADIUS + MCCI_OUTPUT_ROUNDNESS. L'argument OutputOptions peut avoir les valeurs suivantes :
Si l'argument n'est pas spécifié, il est défini à la valeur par défaut MCCI_OUTPUT_CIRCUMSCRIBED_CIRCLE . |
||||||||||||||||||||||
CircleSize |
Spécifie le nombre de valeurs utilisées pour représenter les cercles ajustés. Si vous entrez zéro, le nombre de valeurs d'origine est conservé. L'argument n'est pris en considération que si l'un des cercles énumérés a été sélectionné comme OutputOptions. Les structures de données autorisées sont Scalaire. Tous les types de données entiers sont autorisés. La valeur doit être supérieure ou égale à 0. Si l'argument n'est pas spécifié, il est défini à la valeur par défaut 5000 . |
||||||||||||||||||||||
ConvexHullAlgorithm |
Détermine l'algorithme de l'enveloppe convexe nécessaire au calcul du cercle circonscrit minimum. L'argument ConvexHullAlgorithm peut avoir les valeurs suivantes :
Si l'argument n'est pas spécifié, il est défini à la valeur par défaut CONVEXHULL_GRAHAM_SCAN . |
Remarques
Les valeurs sont converties en points flottants de 64 bits avant que le calcul ne soit effectué.
Dans la première étape, l'enveloppe convexe est calculée à partir du point fixé (voir aussi la fonction ConvexHull). Le cercle circonscrit minimum de l'enveloppe convexe est alors calculé à l'aide de l'algorithme de Skyum [1]. Le temps d'exécution est O(n*log(n)). Le cercle ainsi calculé correspond au cercle circonscrit minimum du point fixé à l'origine.
Les options de résultat de l'argument OutputOptions sont visualisés dans le graphique suivant :
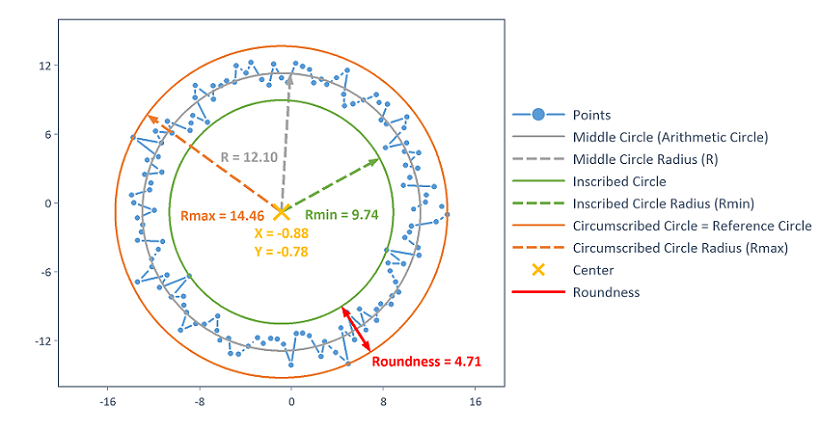
Les résultats sont accessibles en utilisant les noms d'éléments de liste suivants :
Constante |
Signification |
|---|---|
.["Center_X"] |
Coordonnée X du centre du cercle de référence. |
.["Center_Y"] |
Coordonnée Y du centre du cercle de référence. |
.["Middle_Circle"] |
Cercle déterminé arithmétiquement entre le cercle de référence (cercle circonscrit minimum) et le cercle inscrit. |
.["Middle_Circle_Radius"] |
Rayon du cercle moyenné arithmétiquement. |
.["Inscribed_Circle"] |
Le cercle maximum inscrit se rapportant au cercle de référence. |
.["Inscribed_Circle_Radius"] |
Rayon du cercle maximum inscrit par rapport au cercle de référence. |
.["Circumscribed_Circle"] |
Cercle de référence (cercle circonscrit minimum). |
.["Circumscribed_Circle_Radius"] |
Rayon du cercle de référence. |
.["Roundness"] |
L'écart de circularité est la différence entre les rayons des cercles circonscrits et inscrits. |
Vous pouvez aussi toujours utiliser la syntaxe Formula.Listelementname.
Remarque Les calculs de circularité de la MCCI sont basés sur la norme actuellement en vigueur pour déterminer la circularité ; voir [2].
Disponible dans
FlexPro Professional, Developer Suite
Exemples
MinimumCircumscribedCircle(y, x)
Calcule le cercle circonscrit minimum (MCCI) d'un ensemble de points.
MinimumCircumscribedCircle(y, x, MCCI_OUTPUT_ROUNDNESS)
Calcule le cercle circonscrit minimum (MCCI) d'un ensemble de points et ne renvoie que la circularité.
MinimumCircumscribedCircle(points, MCCI_OUTPUT_CIRCUMSCRIBED_CIRCLE_RADIUS + MCCI_OUTPUT_ROUNDNESS)
Calcule le cercle circonscrit minimum (MCCI) d'un ensemble de points. Ainsi, le rayon du cercle déterminé et la circularité sont renvoyés sous forme de liste.
Dim alpha = Series(0, 2*PI, 0.05)
Dim r = 13.5 + Noise(1 # NumberOfRows(alpha), NOISE_NORMAL)
Dim points = Signal(Noise(1) + r*Sin(alpha), Noise(1) + r*Cos(alpha))
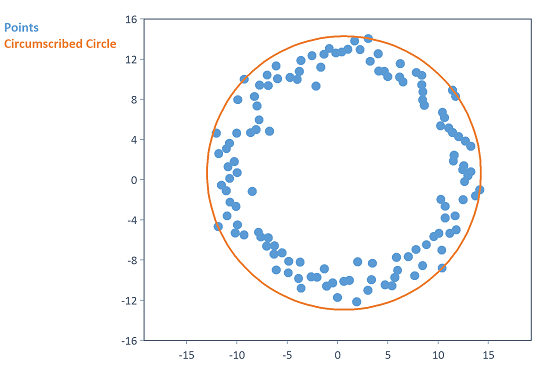
List("Points", points, "Circumscribed Circle", MinimumCircumscribedCircle(points))
Calcule le cercle circonscrit minimum (MCCI) des points répartis de façon aléatoire dans le plan bidimensionnel.
Voir aussi
Fonction MaximumInscribedCircle
Approximation Circulaire - Objet d'analyse
Littérature
[1] Sven Skyum: A simple algorithm for computing the smallest enclosing circle. Dans: Information Processing Letters, Vol. 37, Issue 3, Pages 121-125. https://doi.org/10.1016/0020-0190(91)90030-L,1991.
[2] DIN Deutsches Institut für Normung e.V.: Part 1: Vocabulary and parameters of roundness (ISO 12181-1:2011); English translation of DIN EN ISO 12181-1:2011. Dans: Geometrical product specifications (GPS)- Roundness. 2011.
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations