Algorithme FIR Equiripple
L'inconvénient de la conception de filtres FIR à l'aide de la méthode des fenêtres est que l'erreur d'approximation ne peut pas être influencée dans différentes plages de fréquences. Il est donc souvent préférable, lors de la conception des filtres, d'appliquer la stratégie minimax (minimiser l'erreur maximale) ou un critère d'erreur avec pondération de la fréquence. On obtient ainsi le "meilleur" filtre qui puisse être obtenu pour une spécification donnée.
La méthode FIR Equiripple, également connue sous le nom de méthode Remez Exchange, Parks-McClellan, fournit toujours le filtre FIR avec un effort minimal. La méthode Parks-McClellan fournit la solution pour le filtre FIR en utilisant l'algorithme Remez Exchange dans un processus d'itération. Étant donné que les filtres peuvent être conçus en utilisant cette méthode d'approximation avec une ondulation constante à la fois dans la bande passante et dans la bande d'arrêt, le filtre est également connu sous le nom de filtre Equiripple.
L'algorithme Remez Exchange est un algorithme d'optimisation basé sur les polynômes de Tchebyshev. Une fonction d'erreur est formée pour le filtre souhaité à partir d'une combinaison linéaire de fonctions cosinus et est minimisée par un processus d'optimisation efficace.
Critère de Minimax ou de Tchebyshev
Le critère de Tchebyshev ou Minimax est utilisé pour cette méthode de conception. Pour cette méthode, une recherche est effectuée dans des intervalles de fréquence fixes pour une réponse en fréquence A(ejω) qui minimise l'erreur d'approximation pondérée maximale de la fonction d'erreur. La fonction d'erreur suivante est générée pour cela :
![]()
E(ω) ... fonction d'erreur
W(ω) ... fonction de pondération
H(ejω) ... réponse en fréquence souhaitée
A(ejω) ... fonction d'approximation
La fonction d'erreur, la fonction de pondération et la réponse en fréquence souhaitée ne sont définies que pour des intervalles partiels fermés de la plage de fréquence normalisée 0 <= ω <= 0,5. Par exemple, un filtre passe-bas a les intervalles 0 <= ω <= ωp et ωs <= ω <= 0,5. La fonction d'approximation n'est pas limitée à la largeur de la transition et peut donc prendre n'importe quelle forme, puisqu'aucune limite d'erreur n'est définie ici.
Il est possible de concevoir des filtres dont la réponse en fréquence est librement définie. Pour ce faire, vous pouvez transmettre la réponse en fréquence souhaitée comme un signal dont la composante Y contient les amplitudes sous forme de courbe continue et dont la composante X contient les fréquences normalisées associées (plage de 0 - 0,5).
Principe de l'algorithme d'échange Remez
La procédure est basée sur la reformulation de la tâche de conception du filtre en une tâche d'approximation polynomiale. À l'aide d'une procédure d'itération, une fonction polynomiale claire pn (x) est approximée, qui satisfait aux défauts pn (xi)=yi±h dans une bande d'erreurs ±h. Le polynôme oscille dans la bande d'erreurs dans les extrema locaux de ±h. Vous pouvez choisir le degré polynomial n et la bande d'erreurs ±h. Pour ce faire, on applique le théorème de l'alternance, qui est expliqué en détail dans Oppenheim et Schafer et d'autres ouvrages.
1 Déterminez le polynôme d'ajustement des moindres carrés pn (x) du degré n pour une quantité de n+2 points de données (xi, yi) en résolvant le système d'équations linéaires pour les coefficients polynomiaux a0..an et l'erreur h. Les valeurs de fonction yi (i=1..n+2) à atteindre sont prédéfinies. On obtient donc un système d'équations avec n+2 équations :
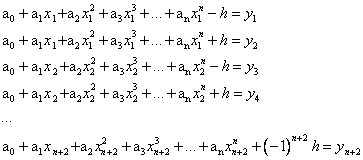
2. Déterminer les n+2 extrema des déviations par rapport à la valeur par défaut.
3. Déterminer le nouveau polynôme d'ajustement des moindres carrés à partir du degré n en utilisant les nouvelles valeurs xi, qui sont aux extrema, comme dans 1.
4. Répétez l'algorithme jusqu'à ce que l'erreur ±h soit suffisante pour les valeurs par défaut.
La procédure est très flexible et peut être utilisée pour obtenir des solutions optimales pour la plupart des filtres non récursifs (par exemple, les filtres passe-bas, passe-haut, passe-bande et multibande avec une réponse en amplitude constante par morceaux, les différentiations numériques et les transformations de Hilbert). Il est même possible de prédéfinir une réponse d'amplitude quelconque et de déterminer le filtre optimal à partir de celle-ci.
L'un des algorithmes informatiques les plus populaires basé sur l'algorithme Remez Exchange est celui de James H. McClellan, Thomas W. Parks et Lawrence R. Rabiner et est également connu sous le nom de méthode Parks-McClellan. L'algorithme utilisé dans FlexPro est basé sur cet algorithme. Avec cet algorithme, vous pouvez concevoir des filtres avec des longueurs de filtre prédéfinies et déterminer des filtres optimaux avec une spécification prédéfinie.
Pondération des erreurs et limites d'erreur
Il existe deux options pour calculer un filtre FIR. Vous pouvez soit spécifier la longueur du filtre, soit prédéfinir une spécification et calculer la longueur du filtre à partir de celle-ci.
Longueur prédéfinie du filtre
Si la longueur du filtre est spécifiée, seul le rapport des erreurs des bandes individuelles peut être défini, car il n'est pas certain que la spécification souhaitée (limites d'erreurs absolues) puisse être préservée en utilisant la longueur de filtre spécifiée.
La longueur prédéfinie du filtre correspond à la longueur de la réponse impulsionnelle. Dans ce cas, la pondération des erreurs des bandes individuelles est spécifiée. Les facteurs de pondération sont en relation les uns avec les autres. Pour un filtre multibande à trois bandes, l'information de pondération {1, 10, 1} signifie, par exemple, que la deuxième bande a une ondulation dix fois plus faible que les deux autres bandes. Cette plage est donc plus lisse. Si la pondération n'est pas spécifiée, toutes les bandes auront le même rapport de pondération.
Spécification prédéfinie
La longueur du filtre n'est pas spécifiée dans ce cas. Au lieu de cela, toutes les limites d'erreur souhaitées sont spécifiées. En utilisant cette information, la longueur du filtre L est estimée empiriquement à l'aide de la formule suivante :

[Source : Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York, p. 701]
Cette formule ne s'applique qu'aux filtres passe-bas et passe-haut. Pour les filtres multibandes, la longueur du filtre est calculée pour chaque transition d'une bande à la suivante. La plus grande valeur est prise comme valeur de départ. Ensuite, la longueur du filtre est augmentée ou réduite jusqu'à ce que le filtre optimal soit déterminé pour la spécification souhaitée.
La procédure ne peut être résolue que numériquement et il s'agit donc d'une procédure relativement intensive pour les ordres supérieurs. Toutefois, il s'agit d'une solution optimale, contrairement à la méthode de la fenêtre. Il est toutefois possible que l'algorithme ne trouve aucune solution en raison de problèmes de convergence.
Références
•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.
•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.
•J. H. McClellan, T. W. Parks, L. R. Rabiner. A Computer Program for Designing Optimum FIR Linear Phase Digital Filters. IEEE Transactions on Audio and Electroacoustics, Vol. AU-21, No.6, December 1973
•L. R. Rabiner, J. H. McClellan and T. W. Parks. FIR Digital Filter Design Techniques Using Chebyshev Approximation. Proceedings IEEE, Vol. 63, No. 4, pp. 595 610, April 1975
Vous serez probablement intéressé par les articles suivants :
Vous êtes actuellement en train de consulter le contenu d'un espace réservé de Facebook. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous devez charger le contenu de reCAPTCHA pour soumettre le formulaire. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de Instagram. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informationsVous êtes actuellement en train de consulter le contenu d'un espace réservé de X. Pour accéder au contenu réel, cliquez sur le bouton ci-dessous. Veuillez noter que ce faisant, des données seront partagées avec des providers tiers.
Plus d'informations