Interspectre et interpériodogramme

L'interspectre et l'interpériodogramme mesurent la puissance spectrale qui est commune à deux signaux.

Le calcul implique la multiplication complexe élément par élément de la première séquence de Fourier avec le conjugué complexe de la seconde séquence de Fourier. La normalisation utilise l'inverse de la longueur des données :

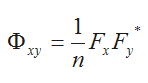
Si on effectue la multiplication complexe conjuguée, on obtient :

(Re{Fx}, Im{Fx}) * (Im{Fx}, Im{Fy}) = (Re{Fx} * Re{Fy} + Im{Fx} * Im{Fy}, Im{Fx} * Re{Fy} + Re{Fx} * Im{Fy})

Le terme réel du résultat contient les composantes en phase du spectre, tandis que le terme imaginaire comprend les composantes spectrales orthogonales.

Le terme réel peut également être écrit comme suit :

Re{Fx} * Re{Fy} + Im{Fx} * Im{Fy} = |Fx| * |Fy| * cos(jxy), avec l'angle de phase jxy entre Fx et Fy.

Tous les formats spectraux réels n'utilisent que la composante réelle. Si les procédures de spectres croisés sont effectuées sur deux signaux identiques, l'interspectre ou l'interpériodogramme générera les mêmes spectres du domaine fréquentiel que le spectre de Fourier ou le périodogramme du signal unique.

L'ordre de x et y n'a d'incidence que sur le signe du terme imaginaire du spectre. L'interspectre de x et y est égal au conjugué complexe de l'interspectre de y et x.

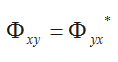
Cohérence

Lorsque deux signaux proviennent de la même source, l'analyse de cohérence permet de mesurer la similarité ou la dépendance linéaire d'un signal par rapport à un autre. La mesure de cohérence la plus couramment utilisée est la magnitude de la cohérence au carré (MSC) :

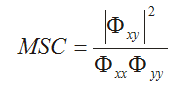
Le tracé de la cohérence varie de 0 à 1. Une cohérence de 0 à une fréquence donnée signifie qu'il n'y a aucune similitude entre les signaux à cette fréquence. Une valeur de cohérence de 1 à une fréquence donnée signifie que le contenu spectral des signaux à cette fréquence est identique. La cohérence entre les signaux x et y est la même que la cohérence entre les signaux y et x.

Spectres du rapport signal/bruit

Si le bruit associé à deux signaux provenant de la même source n'est pas corrélé, comme c'est généralement le cas pour les fonds de bruit blanc, le rapport signal/bruit (SNR) peut être calculé comme suit :

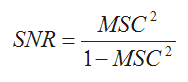
Le SNR, comme la cohérence, est indépendant de l'ordre des séquences x et y.

Fonction de transfert

Pour un signal d'entrée x, le signal renvoyé y est lié par une fonction de transfert qui peut être calculée en utilisant le spectre de puissance du signal d'entrée et le interspectre du signal d'entrée et de sortie :

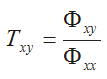
Références

•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.