Cet objet d'analyse vous permet d'approximer un cercle, c'est-à-dire d'effectuer un ajustement de courbe circulaire sur les données sous-jacentes. Utilisez l'approximation circulaire pour analyser les mesures de circularité et pour calculer les vibrations de l'arbre (voir [1], [2], [4]). Les méthodes d'approximation circulaire LSCI, MCCI, MICI, MZCI sont disponibles ainsi qu'une méthode d'approximation de cercle élémentaire (similaire à l'ISO 7919-1 de [3]).

En outre, vous pouvez supprimer les valeurs aberrantes circulaires des données et utiliser un filtre gaussien pour le lissage avant d'effectuer l'approximation circulaire. Les données sous-jacentes sont également désignées ci-après comme le profil.

Description et résultats

Les méthodes d'approximation circulaire LSCI, MCCI, MICI, MZCI calculent un ou plusieurs cercles de référence, qui sont déterminés différemment selon la méthode choisie :

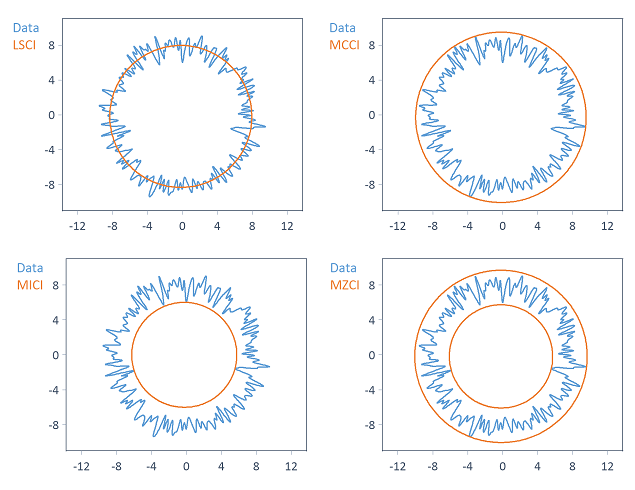
Remarque Selon la méthode d'approximation circulaire sélectionnée, les coordonnées du centre des cercles de référence diffèrent plus ou moins les unes des autres.

Le cercle central, le cercle inscrit et le cercle circonscrit sont dérivés du ou des cercles de référence et calculés (chacun ayant le même centre que le cercle de référence). L'objet d'analyse peut renvoyer les cercles, les paramètres statistiques (par exemple, les rayons des cercles et les coordonnées du centre des cercles) et les données préfiltrées comme résultats. Vous pouvez spécifier le nombre de valeurs des cercles comme paramètres.

Dans tous les cas, la circularité est disponible en tant que paramètre statistique (également appelé écart de circularité ). Elle est toujours calculée comme la différence entre le rayon du cercle circonscrit et le rayon du cercle inscrit (et est donc une quantité dérivée du cercle de référence respectif). L'écart de circularité est une mesure de l'arrondi du profil mesuré. Pour la méthode LSCI et la méthode d'approximation du cercle élémentaire(détermination du centre du cercle par la moyenne de la trajectoire circulaire), des paramètres statistiques supplémentaires sont calculés et édités comme décrit ci-dessous.

La figure suivante visualise les cercles renvoyés et les paramètres statistiques pour l'exemple de la méthode d'approximation des cercles LSCI :

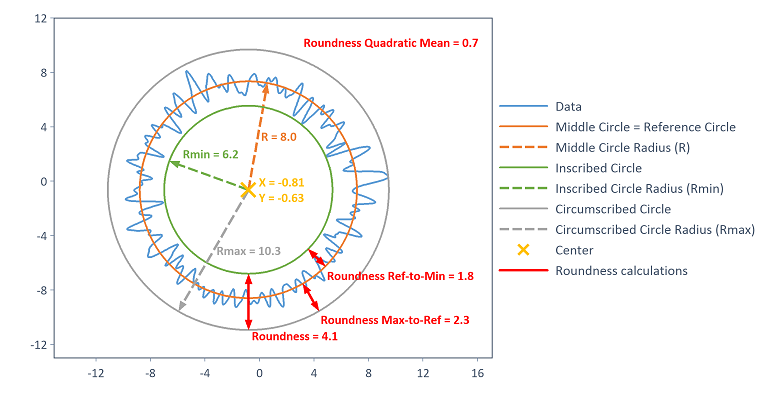
LSCI - Cercle des moindres carrés

Le calcul du cercle de référence LSCI est basé sur la fonction LeastSquaresCircle. Le cercle LSCI est calculé comme le cercle auquel la somme des carrés des écarts par rapport aux données devient minimale. Dans la littérature de référence, on parle de cercle de Gauss. Le cercle inscrit est alors fourni comme le cercle inscrit maximum par rapport au centre du cercle LSCI. Le cercle de référence est fourni comme le cercle circonscrit minimum par rapport au centre du cercle LSCI. Le cercle circonscrit correspond au cercle de référence, c'est-à-dire le cercle LSCI.

Les deux algorithmes suivants sont disponibles pour calculer le cercle LSCI :

Dans la méthode LSCI, en plus de l'écart d'arrondi, l'écart d'arrondi entre le pic et la référence (différence entre le rayon du cercle circonscrit et le rayon du cercle de référence), l'écart d'arrondi entre la référence et la vallée (différence entre le rayon du cercle de référence et le rayon du cercle inscrit) ainsi que la moyenne quadratique des écarts des points de données par rapport au cercle de référence sont produits comme paramètres statistiques (voir [1]).

MCCI - Cercle circonscrit minimum

Le calcul du cercle de référence MCCI est basé sur la fonction MinimumCircumscribedCircle. Dans cette méthode, le cercle de référence est calculé comme le cercle ayant le plus petit diamètre possible qui peut être placé sur le profil depuis l'extérieur. On l'appelle aussi cercle circonscrit minimal. Le cercle circonscrit dans cette méthode correspond au cercle de référence. Le cercle inscrit est fourni comme le cercle inscrit maximum par rapport au centre du cercle de référence. Dans ce cas, le cercle central est également défini comme le cercle à moyenne arithmétique entre le cercle de référence (c'est-à-dire le cercle circonscrit) et le cercle inscrit.

Pour calculer le cercle MCCI, l'algorithme sous-jacent nécessite le calcul de la coque convexe. L'enveloppe convexe peut être calculée à l'aide de l'une des deux méthodes suivantes :

MICI - Cercle inscrit maximum

Le calcul du cercle de référence MICI est basé sur la fonction MaximumInscribedCircle. Dans cette méthode, le cercle de référence est calculé comme le cercle avec le plus grand diamètre possible qui peut être placé sur le profil depuis l'intérieur. On l'appelle aussi cercle inscrit maximal. Le cercle inscrit dans cette méthode correspond au cercle de référence lui-même. Le cercle circonscrit apparaît comme le cercle circonscrit minimum par rapport au centre du cercle de référence. Dans ce cas, le cercle central est défini comme le cercle à moyenne arithmétique entre le cercle circonscrit et le cercle de référence (c'est-à-dire le cercle inscrit).

MZCI - Cercles de zone minimum

Deux cercles de référence sont déterminés dans la méthode MZCI. Le calcul est basé sur la fonction MinimumZoneCircle. Dans ce cas, on détermine deux cercles concentriques qui englobent le profil d'arrondi et présentent la plus petite distance radiale possible l'un par rapport à l'autre. Les cercles de référence sont constitués du cercle circonscrit et du cercle inscrit. Dans ce cas, le cercle central est défini comme le cercle à moyenne arithmétique entre les deux cercles de référence, c'est-à-dire le cercle circonscrit et le cercle inscrit.

Pour calculer le cercle MZCI, les itérations supplémentaires sont dérivées des paramètres d'incrémentation sont utilisées. Il est utile de comprendre l'algorithme MZCI afin de pouvoir déclarer les paramètres : Les cercles de référence concentriques de la zone minimale sont estimés lors de la première étape d'itération par les cercles inscrits et circonscrits calculés par le cercle des moindres carrés (LSCI). Le résultat est ensuite amélioré de façon itérative. Un nouveau point est sélectionné autour du point central des cercles concentriques inscrits et circonscrits actuels à l'aide d'une distribution normale bidimensionnelle (l'écart-type correspond à l'Incrément). Un contrôle détermine si les cercles concentriques inscrits et circonscrits recalculés sur le nouveau point ont une différence de rayon moins importante qu'auparavant. Si c'est le cas, le point devient le nouveau point central. La procédure est maintenant répétée itérativement n fois selon la valeur du paramètre Itérations et les cercles de la zone minimale sont ainsi améliorés successivement.

Les options suivantes sont disponibles pour les paramètres Itérations et Incrément:

détermination du centre du cercle en faisant la moyenne de la trajectoire circulaire

Cette méthode d'approximation du cercle est très simple et consiste à déterminer le centre du cercle en faisant la moyenne des composantes X et Y. Le centre du cercle est donc déterminé a priori. Un cercle de référence n'est donc pas déterminé par cette méthode. Le cercle de référence apparaît comme le cercle circonscrit minimum par rapport au centre du cercle calculé. Le cercle inscrit apparaît comme le cercle inscrit maximum par rapport au centre du cercle calculé. Le rayon du cercle central correspond à la valeur moyenne des distances des points de données par rapport au centre du cercle. Cela définit le cercle central. Il convient de noter que le cercle central calculé de cette manière peut être interprété comme la valeur estimée (initiale) du cercle LSCI (et produit des résultats similaires). L'utilisation de cette méthode n'a donc de sens que lorsque les données sous-jacentes sont échantillonnées périodiquement (profil fermé).

Si un ou plusieurs cercles de référence ont été sélectionnés comme résultat, tous les cercles seront produits (c'est-à-dire le cercle inscrit, le cercle central et le cercle circonscrit), car il n'existe pas de cercle de référence explicite pour cette méthode.

Note Cette méthode d'approximation du cercle élémentaire suit la procédure de la norme ISO 7919-1, où le centre du cercle est également calculé en faisant la moyenne des composantes X et Y (voir [3]). Cependant, veuillez noter qu'aucun cercle inscrit, central et circonscrit n'est défini dans la norme ISO-7919-1 et que, par conséquent, l'écart de circularité, tel que spécifié ci-dessus, n'a pas été calculé. Comme les méthodes mentionnées ci-dessus, les cercles inscrits, centraux et circonscrits ainsi que l'écart de circularité sont fournis ici comme résultats pour des raisons de symétrie et de comparaison.

En outre, d'autres quantités statistiques sont produites, qui sont énumérées dans la norme ISO 7919-1 comme mesure pour le calcul de la trajectoire de l'arbre. Ce sont :

Préfiltrage par élimination des valeurs aberrantes circulaires

Avant d'effectuer l'approximation circulaire, les aberrations circulaires peuvent être éliminées des données. Tous les points de données dont la distance par rapport au centre du cercle spécifié est supérieure au rayon minimum réglable et inférieure au rayon maximum réglable sont supprimés :

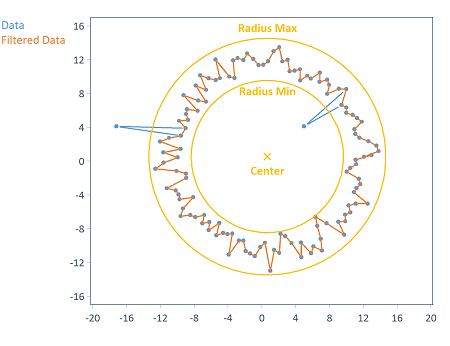
Les coordonnées X et Y du centre du cercle peuvent être calculées automatiquement (comme la moyenne des composantes X et Y respectives des données d'entrée) ou spécifiées explicitement.

Préfiltrage avec un filtre gaussien

Avant d'effectuer l'approximation circulaire, le profil de circularité peut être préfiltré à l'aide d'un filtre gaussien (voir [2]). La fonction GaussianFilter est utilisée à cet effet. Pour des raisons mathématiques, les données sous-jacentes doivent être échantillonnées périodiquement pour le filtrage (c'est-à-dire le profil fermé).

Le filtre gaussien est généralement utilisé dans ce cas pour lisser le profil (paramètre type de filtre: Passe-bas). Comme [2], le filtre gaussien peut également être utilisé pour le filtrage passe-haut du profil. Un filtre passe-bande gaussien peut être mis en œuvre en exécutant consécutivement un filtre passe-bas et un filtre passe-haut.

Spécifiez la fréquence de coupure pour le filtrage dans l'unité UPR (Undulations Per Revolution). Par exemple, 150 UPR correspond à la 150e vibration harmonique de la fréquence fondamentale. La fréquence fondamentale (normalisée) doit également être spécifiée. C'est l'inverse du nombre de points de données par révolution. Les options suivantes sont disponibles pour spécifier le Nombre de points de données par révolution:

L'illustration suivante montre un profil lissé avec un filtre gaussien (c'est-à-dire un filtrage passe-bas) avec une fréquence de coupure de 50 UPR :

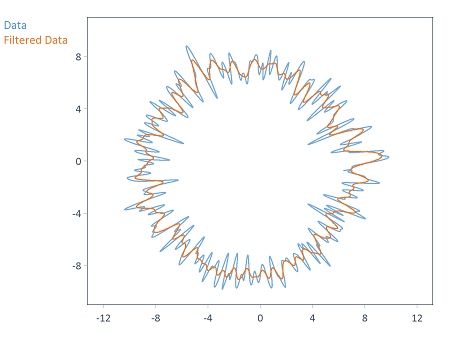
Données en coordonnées polaires

Les données d'entrée peuvent être présentes à la fois en coordonnées cartésiennes et en coordonnées polaires (rayon et angle). Vous pouvez le saisir dans l'onglet Données de l'objet d'analyse. La composante Y est ici le rayon et la composante X est l'angle.

Les paramètres suivants sont disponibles pour l'unité d'angle:

Si une représentation en coordonnées polaires est présente, les données sont transformées en coordonnées cartésiennes avant le calcul.

Les résultats, en revanche, sont toujours émis en coordonnées cartésiennes. Vous pouvez les transformer en un graphique polaire pour la présentation comme le montre l'exemple suivant :

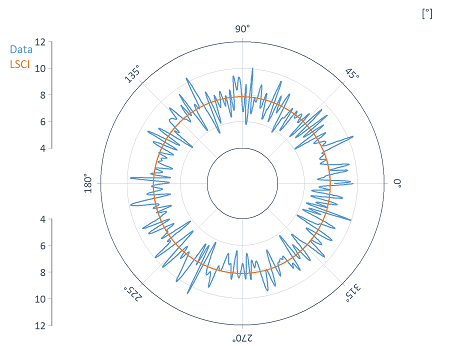
Références

[1] DIN Deutsches Institut für Normung e.V.Part 1: Vocabulary and parameters of roundness (DIN EN ISO 12181-1:2011),Geometrical product specifications (GPS)- Roundness, 2011.

[2] DIN Deutsches Institut für Normung e.V.Part 2: Specification operators (DIN EN ISO 12181-2:2011),Geometrical product specifications (GPS)- Roundness, 2011.

[3] DIN Deutsches Institut für Normung e.V. Measurements on rotating shafts and evaluation criteria, Part 1: General guidelines (DIN ISO 7919-1:1996), 1996.

[4] Verein Deutscher Ingenieure. Form measurement - Principles for the measurement of geometrical deviations (VDI/VDE 2631), 1999.]

Fonctions FPScript utilisées

LeastSquaresCircle

MaximumInscribedCircle

MinimumCircumscribedCircle

MinimumZoneCircle

GaussianFilter

Frequency

ValuesInInterval

Voir aussi

ConvexHull

* Cet objet d'analyse n'est pas disponible dans FlexPro View et FlexPro Basic.