HarmonicRemovalFilter (FPScript)
Removes harmonic components from time signals (harmonic removal). To do this, the data is converted from the time domain to the revolution domain, where cycle averaging and subtraction provides the desired harmonic removal.
Syntax
HarmonicRemovalFilter(Signal, SpeedOrFundamentalFrequency, [ OrderForHarmonicRemoval = 1 ], [ NumberOfCyclesForAveraging = 15 ], [ SamplesPerRevolution = 512 ] [ , OutputOptions = HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN ])
The syntax of the HarmonicRemovalFilter function consists of the following parts:
Part |
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
Signal |
The signal sampled over time from which harmonic components (harmonics) are to be removed. The unit of the X component must be compatible with the seconds unit (with Unit Monitoring switched on). If no unit of the X component is specified or Unit Monitoring is switched off, the unit is always interpreted in seconds. Permitted data structures are signal. All real data types are permitted, except Boolean value, calendar time und time span. Void values are not permitted in this argument. For the X component additional restrictions do apply.The values must be monotonously increasing. Void values are not permitted in this argument. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
SpeedOrFundamentalFrequency |
The underlying rotating component for harmonic removal as a speed signal sampled over time (from which the revolution domain for harmonic removal is derived). Alternatively, it is the underlying fixed fundamental frequency. The unit of the Y component must be compatible to the unit 1/min (or to RPM = revolutions per minute) (when Unit Monitoring is switched on). If no unit of the Y component is specified or Unit Monitoring is switched off, the unit is always interpreted as 1/min. The unit of the X component must be compatible with the seconds unit (with Unit Monitoring switched on). If no unit of the X component is specified or Unit Monitoring is switched off, the unit is always interpreted in seconds. The sampling rate does not necessarily have to match the sampling rate of Signal. If it is a scalar value, then it is assumed that the signal to be filtered was recorded at this constant speed or that harmonic components related to multiples of this fixed fundamental frequency are to be extracted. Permitted data structures are scalar value und signal. All real data types are permitted, except Boolean value, calendar time und time span. The argument is transformed to the unit min^-1. Void values are not permitted in this argument. For the X component additional restrictions do apply.The values must be monotonously increasing. Void values are not permitted in this argument. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
OrderForHarmonicRemoval |
Defines the order (i.e. multiples of the speed or multiples of the fundamental frequency) to be removed from the time signal along with all harmonic components. For example, choosing 4 means that orders 4, 8, 12, 16, 20, etc. are removed. Permitted data structures are scalar value. All numeric data types are permitted. The value must be greater than 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value 1. |
||||||||||
NumberOfCyclesForAveraging |
For harmonic removal, the signal to be filtered is first transformed into the revolution domain, where moving cycle averaging and subtraction is performed. This value determines the number of cycles to be averaged in the revolution domain in order to calculate the respective averaged harmonic order. The larger the value, the greater the filter selectivity. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 2. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value 15. |
||||||||||
SamplesPerRevolution |
For harmonic removal, the signal to be filtered is first transformed into the revolution domain. This value determines the sampling of the signal transformed into the revolution domain (number of data points per revolution). Half of the value determines the maximum order that can even be calculated using Fourier analysis according to the sampling theorem. A value should therefore be chosen so that all orders above half of that value are negligibly small. Otherwise, aliasing occurs (according to the sampling theorem). Smaller values, on the other hand, reduce the algorithm's calculation time. The value should also be set so that SamplesPerRevolution / OrderForHarmonicRemoval is an integer. If the latter condition is not fulfilled, approximated values for the number of data points per revolution and the order to be filtered are automatically calculated, which fulfill this condition. The approximated value calculated by the algorithm for the order to be filtered then matches OrderForHarmonicRemoval except by at least 2 decimal places. The approximated value calculated by the algorithm for the number of data points per revolution in this case is limited on the downside by the value of SamplesPerRevolution. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 1. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value 512. |
||||||||||
OutputOptions |
Specifies which results are to be returned. Multiple results are output as a list. If, for example, the signal filtered in the revolution domain (without harmonics) as well as the filtered time signal transformed back into the time domain are to be output, then the argument must contain the value HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_REVOLUTION_DOMAIN + HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN. The argument OutputOptions can have the following values:
If this argument is omitted, it will be set to the default value HARMONICREMOVALFILTER_OUTPUT_SIGNAL_IN_TIME_DOMAIN. |
Remarks
The algorithm of the transformation procedure can be described schematically as follows (for example, see [1], [2], or [3]):
1) Transformation into the revolution domain: First Signal is transformed from the time domain into the revolution domain (analogous to the procedure of the RevolutionSyncSampling function, where a linear transformation is chosen here). The revolution domain is calculated here in particular from the argument SpeedOrFundamentalFrequency. In addition, the transformation requires arguments necessary for the RevolutionSyncSampling function with regard to the number of data points per revolution.
2) Cycle averaging: In the revolution domain, a (moving) average is calculated over a user-defined number of cycles. Everything that rotates in sync with the wave is a harmonic that is included in this cycle of averages. Components that rotate non-synchronously with the first order wave are averaged out. Therefore, the average cycle consists of data that are synchronous and harmonic with the underlying tachometer (i.e. with SpeedOrFundamentalFrequency). In a four-stroke engine, for example, there is one combustion event for every two revolutions of the crankshaft. One cycle therefore consists of 2 revolutions. If the combustion event, including the harmonic components, are to be removed here, then OrderForHarmonicRemoval must be set to the value 0.5.
3) Cycle subtraction: The (moving) average cycle is then subtracted from each cycle in order to perform the desired harmonic removal. The result is then the signal filtered in the revolution domain (without harmonics of the filtered out order).
4) Transformation back into the time domain: The signal filtered in the revolution domain is then transformed back into the time domain.
As an example, consider the order spectrum of a time signal calculated from a run-up:
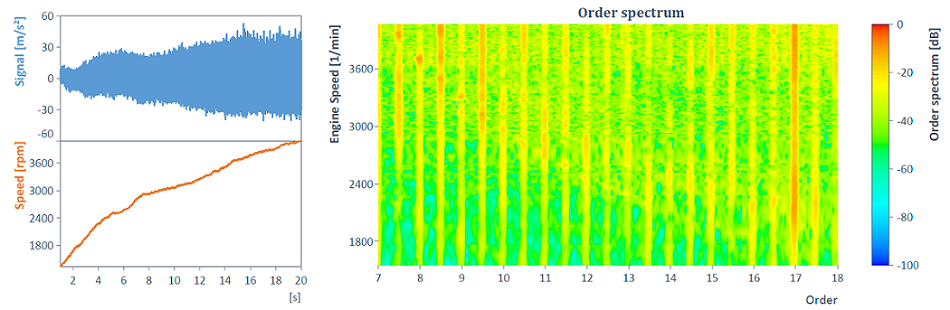
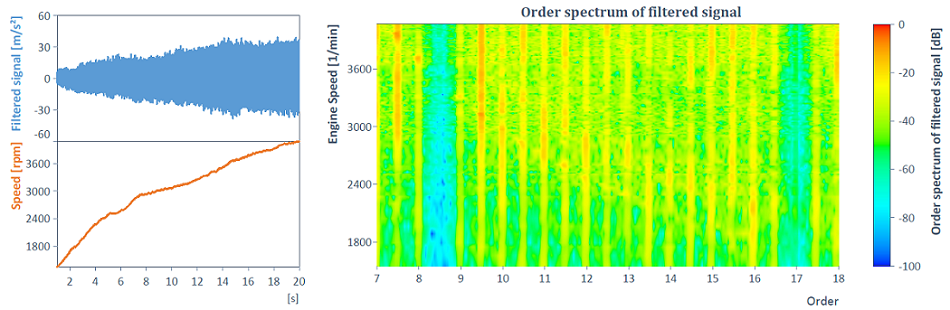
For example, with the help of the underlying HarmonicRemovalFilter function, order 8.5 can be removed together with all harmonic components:
If the result is a list, the results can be accessed with the following list element names:
Constant |
Description |
|---|---|
.["Signal_over_Time"] |
The filtered signal (without harmonics) transformed back into the original time domain. |
.["Signal_over_Revolutions"] |
The filtered signal (without harmonics) transformed into the revolution domain. |
.["Speed_over_Revolutions"] |
The speed signal transformed into the revolution domain. |
.["Time_over_Revolutions"] |
The (non-equidistant) time points associated with the revolution sampling points. |
You can also always use the syntax Formulaname.Listelementname.
Note According to the sampling theorem, theoretically all orders up to orderMax = 0.5*SamplingRate(Signal)/Maximum(Speed) can be detected and analyzed. SamplesPerRevolution should be set to a value greater than twice the value of orderMax.
Available in
Option Order Tracking
Examples
HarmonicRemovalFilter(Signal, Speed, 8.5)
Removes the 8.5th order (related to the speed signal) together with all harmonic components. The result is the time domain filtered signal (without the corresponding harmonics)
HarmonicRemovalFilter(Signal, 12 Hz, 1)
Removes the 12 Hz fundamental frequency and its harmonic components in a signal. The result is the signal filtered in the time domain.
Dim SyncSampling = RevolutionSyncSampling(Signal, Speed, 512,,,,REVSYNCSAMPLING_OUTPUT_ALL) // Step 1: transform to rev. domain
Dim n = 512/4
Dim cycles = Reshape(SyncSampling.["Signal_over_Revolutions"], {NumberOfRows(SyncSampling.["Signal_over_Revolutions"])/n, n})
Dim avgeragedCycles = Mean(cycles, MEAN_ARITHMETIC + PROCESS_ROWS + CALC_MOVING, 25) // Step 2: cycle averaging
Dim harmonicRemoval = Signal(Reshape(cycles - avgeragedCycles), SyncSampling.["Time_over_Revolutions"]) // Step 3: cycle substraction
RemoveVoidValues(Sample(harmonicRemoval, Signal.X)) // step 4: transform back to time domain
Equivalent FPScript code to HarmonicRemovalFilter(Signal, Speed, 4, 25, 512).
See Also
RevolutionSyncSampling Function
Harmonic Filter Analysis Object
Revolution Synchronous Order Tracking Analysis Object
Revolution Synchronous Sampling Analysis Object
References
[1] B. Peeters, B. Cornelis, K. Janssens, H. Van der Auweraer: Removing disturbing harmonics in Operational Modal Analysis. In: Proceedings of the International Operational Modal Analysis Conference IOMAC, Copenhagen, Denmark. 2007.
[2] R.B. Randall: State of the art in monitoring rotating machinery. In: Proceedings of the International Seminar on Modal Analysis ISMA, Leuven, Belgium. 2002.
[3] E. Bechhoefer, M. Kingsley: A Review of Time Synchronous Average Algorithms. In: Proceedings of the Annual Conference of the Prognostics and Health Management Society, San Diego, USA. 2009.