Cross Spectrum and Cross Periodogram

The Cross Spectrum and the Cross Periodogram measure the spectral power that is common across two signals.

The computation involves the element by element complex multiplication of the first Fourier sequence with the complex conjugate of the second Fourier sequence. The normalization uses the inverse of the data length:

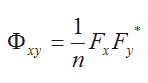
If the conjugated complex multiplication is performed, this results in:

(Re{Fx}, Im{Fx}) * (Im{Fx}, Im{Fy}) = (Re{Fx} * Re{Fy} + Im{Fx} * Im{Fy}, Im{Fx} * Re{Fy} + Re{Fx} * Im{Fy})

The real term of the result contains the in-phase components of the spectrum while the imaginary term includes the orthogonal spectral components.

The real term can also be written as:

Re{Fx} * Re{Fy} + Im{Fx} * Im{Fy} = |Fx| * |Fy| * cos(jxy), with the phase angle jxy between Fx and Fy.

All real spectral formats only use the real component. If the cross-spectra procedures are performed on two identical signals, the cross-spectrum or cross-periodogram will generate the same frequency domain spectra as the single signal Fourier Spectrum or Periodogram.

The order of x and y impacts only the sign of the imaginary term in the spectrum. The cross spectrum of x and y is equal to the complex conjugate of the cross spectrum of y and x.

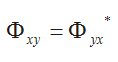
Coherence

When two signals arise from the same source, Coherence analysis offers the measure of similarity or linear dependence of one signal on another. The most commonly used measure of coherence is the magnitude squared coherence (MSC):

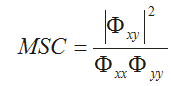
The coherence plot will vary from 0 to 1. A coherence of 0 at a given frequency means there is no similarity between the signals at this frequency. A coherence value of 1 at a given frequency means the spectral content in the signals at this frequency are identical. The coherence between signals x and y is the same as the coherence between signals y and x.

Signal to Noise Ratio Spectra

If the noise associated with two signals from the same source is uncorrelated, as is generally the case for white noise backgrounds, the Signal to Noise Ratio (SNR) can be computed as follows:

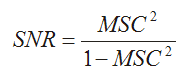
The SNR, like the coherence, is independent of the x and y sequence order.

Transfer Function

For an input signal x, the output signal y is related by a Transfer Function that can be computed using the power spectrum of the input signal and the cross-spectrum of the input and output signal:

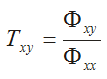
References

•Oppenheim, A. V. and Schafer, R. W. (1989). Discrete-Time Signal Processing. Prentice Hall, Englewood Cliffs, NJ.