Low pass filters, which filter out higher frequencies, are often used for smoothing data. High frequency oscillations - especially measuring errors - are minimized by doing this.

Unlike most low pass filters used in the Fourier domain, the Savitzky-Golay filter is used in the time domain. Imagine the filter as a window that moves across the data and assigns a mean value to each data point across the associated window (moving window averaging):

gi is the filtered value at the position i.

fj is the unfiltered value at the position j.

nL specifies the data points to the left of the point to be smoothed.

nR specifies the data points to the right of the point to be smoothed.

cn is the weighting function.

The SavitzkyGolay filter method performs a local polynomial regression in order to determine the smoothed values for each data point. This method is superior to that of the moving average, since it maintains data attributes such as impulse amplitude and length that are usually degraded by the moving average. The method is especially used when a peak has been sampled through only a few points. The position and height of the peak can be estimated, even if the maximum falls between two sampling points.

The coefficients cn are selected so that the higher moments are preserved. Unlike the moving average, the coefficients are not calculated by a constant (estimated by the mean value), but are provided by a higher order polynomial. A least squares estimation is used for the calculation. Fortunately, it is not necessary to recalculate the coefficients for each point. The calculation is actually independent of the real data and depends only on the degree of the polynomial. Fitting is performed through a least squares estimation (LS estimation) between the matrix A and vector f:

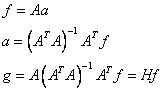
H is also called the "hat" matrix and is the same for each f for a given polynomial. It can also make the calculation once and save it for later use. To calculate the coefficients, only one row of the inverse matrix has to be calculated. This can be obtained, for instance, from the LU decomposition using only one back substitution.

Note: The Savitzky-Golay smoothing method is also called the Digital Smoothing Polynomial Filter (DISPO).

References

•Savitzky A., and Golay, M.J.E. (1964). Analytical Chemistry, vol. 36, p. 1627–1639.

•W. H. Press, et. al. (1992). Numerical Recipes in C, Second Edition. Cambridge University Press, p. 650-655.