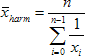Mean (FPScript)
Determines individual, floating or block mean values for a data set.
Syntax
Mean(DataSet, [ Mode = MEAN_ARITHMETIC + PROCESS_ROWS ] [ , IntervalWidth ])
The syntax of the Mean function consists of the following parts:
Part |
Description |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
The data set to be searched. All data structures are allowed. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||||||||||||||||||||
Mode |
Selects the type of mean. Specifies how data matrices and signal series should be processed and whether individual, floating or block mean values are to be determined. The argument Mode can have the following values:
...plus a constant, which determines the processing of data matrices and signal series....
... plus an optional constant, which determines the type of mean.
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value MEAN_ARITHMETIC + PROCESS_ROWS. |
||||||||||||||||||||||||
IntervalWidth |
This argument is required to determine floating and block mean values. The interval width then specifies the number of values to be examined. The width should be an odd number. Otherwise, the interval is asymmetrical, and one more value is included in the calculation to the right of the center as opposed to the left. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 1. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
Remarks
A scalar value is returned without modification. For signals and signal series, the Y component is processed and the X or Z component is copied, if possible. For the calculation of floating and block mean values, the data structure of the result corresponds to that of the argument. If, on the other hand, DataSet is a data series or a signal, the result is a scalar value with the mean value searched for. Otherwise, the result is a data series or a signal with one mean value per column or row.
The data type of the result is always a real floating point value.
Available in
FlexPro View, Basic, Professional, Developer Suite
Examples
Mean({2, 5, 8, 6, 4}) |
Results in 5. |
Mean({1, 2, 3, 4, 5, 6}, PROCESS_COLUMNS + CALC_MOVING, 3) |
Results in {1.5, 2, 3, 4, 5, 5.5}. |
Mean({1, 2, 3, 4, 5, 6}, PROCESS_COLUMNS + CALC_BLOCK, 3) |
Results in {2, 5}. |
See Also
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information