MaximumInscribedCircle (FPScript)
Calculates the maximum inscribed circle (MICI) of a two-dimensional point set. Used to determine roundness.
Syntax
MaximumInscribedCircle(Points, [ OutputOptions = MICI_OUTPUT_INSCRIBED_CIRCLE ] [ , CircleSize = 5000 ])
or
MaximumInscribedCircle(Y, X, [ OutputOptions = MICI_OUTPUT_INSCRIBED_CIRCLE ] [ , CircleSize = 5000 ])
The syntax of the MaximumInscribedCircle function consists of the following parts:
Part |
Description |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Points |
The Y and X points for which the maximum inscribed circle is to be calculated. The same unit must be used for both components of the signal. Permitted data structures are signal. All real data types are permitted, except calendar time und time span. |
||||||||||||||||||||||
Y |
The Y points used to calculate the maximum inscribed circle. If you specify a signal, its Y component is used. The unit must match the unit of the X argument. Permitted data structures are data series und signal. All real data types are permitted, except calendar time und time span. |
||||||||||||||||||||||
X |
The X points used to calculate the maximum inscribed circle. If you specify a signal, its Y component is used. The unit must match the unit of the Y argument. Permitted data structures are data series und signal. All real data types are permitted, except calendar time und time span. |
||||||||||||||||||||||
OutputOptions |
Specifies which results are to be returned. Multiple results are output as a list. If, for instance, the radius of the reference circle and the roundness should be output, the argument must contain the value MICI_OUTPUT_INSCRIBED_CIRCLE_RADIUS + MICI_OUTPUT_ROUNDNESS. The argument OutputOptions can have the following values:
If this argument is omitted, it will be set to the default value MICI_OUTPUT_INSCRIBED_CIRCLE. |
||||||||||||||||||||||
CircleSize |
Specifies the number of values used to represent the fitted circles. If you enter zero, the original number of values are retained. The argument is considered only if one of the listed circles was selected for OutputOptions. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 0. If this argument is omitted, it will be set to the default value 5000. |
Remarks
The values are converted to 64-bit floating points before the calculation is made.
In the first step, the Delaunay triangulation is calculated from the point set in order to generate a triangular mesh (triangulation) from the point set (algorithm used with run time O(n*log(n)): randomized incremental construction from [1]). The maximum inscribed circle is then the circle with the maximum circumference of all triangles contained in the triangulation.
The output options of the argument OutputOptions are visualized in the following diagram:
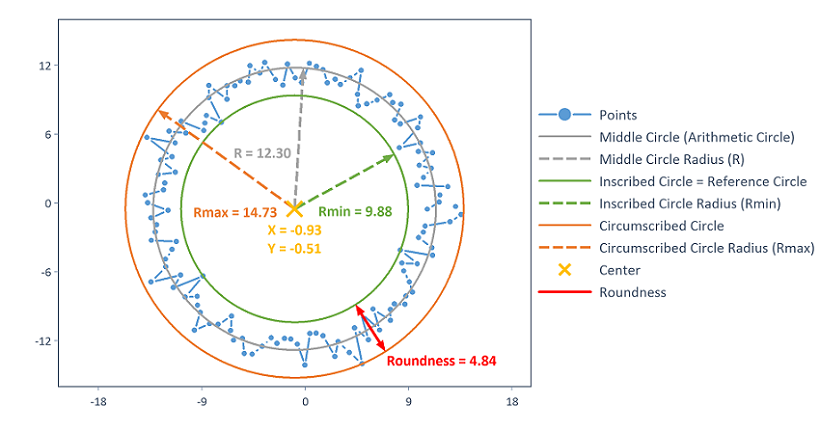
The results can be accessed using the following list element names:
Constant |
Meaning |
|---|---|
.["Center_X"] |
X coordinate of the center of the reference circle. |
.["Center_Y"] |
Y coordinate of the center the reference circle. |
.["Middle_Circle"] |
Arithmetically averaged circle between the reference circle (maximum inscribed circle) and the circumscribed circle. |
.["Middle_Circle_Radius"] |
Radius of the arithmetically averaged circle. |
.["Inscribed_Circle"] |
Reference circle (maximum inscribed circle). |
.["Inscribed_Circle_Radius"] |
Radius of the reference circle. |
.["Circumscribed_Circle"] |
The minimum circumscribed circle related to the reference circle. |
.["Circumscribed_Circle_Radius"] |
Radius of the minimum circumscribed circle related to the reference circle. |
.["Roundness"] |
Roundness deviation as the difference between the radii of the circumscribed and inscribed circles. |
You can also always use the Formula.Listelementname syntax.
Note The MICI roundness calculations are based on the currently valid standard for determining roundness; see [2].
Available in
FlexPro Professional, Developer Suite
Examples
MaximumInscribedCircle(y, x)
Calculates the maximum inscribed circle (MICI) of a point set.
MaximumInscribedCircle(y, x, MICI_OUTPUT_ROUNDNESS)
Calculates the maximum inscribed circle (MICI) of a point set and returns only the roundness.
MaximumInscribedCircle(points, MICI_OUTPUT_INSCRIBED_CIRCLE_RADIUS + MICI_OUTPUT_ROUNDNESS)
Calculates the maximum inscribed circle (MICI) of a point set. As the result, the radius of the determined circle and the roundness are output as a list.
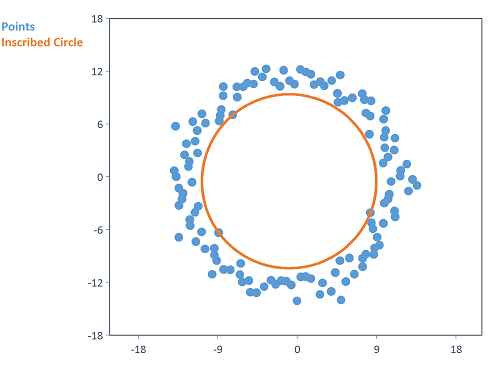
Dim alpha = Series(0, 2*PI, 0.05)
Dim r = 13.5 + Noise(1 # NumberOfRows(alpha), NOISE_NORMAL)
Dim points = Signal(Noise(1) + r*Sin(alpha), Noise(1) + r*Cos(alpha))
List("Points", points, "Inscribed Circle", MaximumInscribedCircle(points))
Calculates the maximum inscribed circle (MICI) of randomly distributed points in the two-dimensional plane.
See Also
MinimumCircumscribedCircle Function
Circle Approximation - Analysis Object
References
[1] Leonidas J. Guibas, Donald E. Knuth, and Micha Sharir: Randomized Incremental Construction of Delaunay and Voronoi Diagrams. In: Algorithmica, Vol. 7, Pages 381-413. https://link.springer.com/article/10.1007/BF01758770,1992.
[2] DIN Deutsches Institut für Normung e.V.: Part 1: Vocabulary and parameters of roundness (ISO 12181-1:2011); English translation of DIN EN ISO 12181-1:2011. In: Geometrical product specifications (GPS)- Roundness. 2011.
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information