Multiplies matrices with vectors and matrices in all combinations.

Syntax

MatrixMultiplication(A, B)

The syntax of the MatrixMultiplication function consists of the following parts:

Remarks

The unit of the result is the same as the product of the units of A and B. The arguments A and B provide the matrices or vectors to be multiplied. In this case, matrices are provided as data matrices whose data series correspond to the rows. Vectors are provided as data series.

For complex arguments, complex multiplication takes place and the result is also complex. The result always has the same data type as the arguments. If the arguments have different data types, then these are adapted to each other in such a way that there is no loss of resolution in the result, i.e. lower resolutions are converted into higher resolutions, integers into floating point values and real numbers to complex numbers.

The complex multiplication is defined as (a, b) * (c, d) = (a * c - b * d, a * d + b * c).

The result has the same data type as the eventually transformed argument. The following operations are performed:

Vector with Vector: The scalar product of the two vectors A and B is formed.

Example for vectors with three elements:

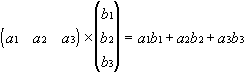
Matrix with Vector: Each row in the matrix A is subjected to vector multiplication with the vector B. The number of rows in matrix A must match the number of elements in vector B.

Example for a 3x3 matrix A and vector B with three elements:

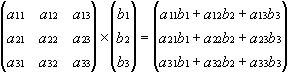
Vector with Matrix: Each column in matrix B is subjected to vector multiplication with the vector A, where the number of columns in the matrix must match the number of vector elements.

Example for a 3x3-matrix and a vector with three elements:

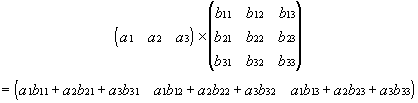
Matrix with Matrix: Each row in the matrix A is subjected to vector multiplication with each column in matrix B. The number of rows in the matrix A must match the number of columns in matrix B.

Example for two 3x3 matrices:

If the argument is a list, then the function is executed for each element of the list and the result is also a list.

Note        Note that the data series in the data matrix are interpreted as the matrix rows, although these are displayed as columns in the data set window. This assignment is required so that the Index Operator can be applied for matrices in the order defined in Linear Algebra where the first index value specifies the row and the second one specifies the column.

Available in

FlexPro Basic, Professional, Developer Suite

Examples

See Also

InverseMatrix Function

TransposeMatrix Function