LeastSquaresCircle (FPScript)
Calculates the least squares circle (LSCI) of a two-dimensional point set (least squares reference circle). Used to determine roundness.
Syntax
LeastSquaresCircle(Points, [ OutputOptions = LSCI_OUTPUT_MIDDLE_CIRCLE ], [ CircleSize = 5000 ] [ , Algorithm = LSCI_ALGORITHM_KASA ])
or
LeastSquaresCircle(Y, X, [ OutputOptions = LSCI_OUTPUT_MIDDLE_CIRCLE ], [ CircleSize = 5000 ] [ , Algorithm = LSCI_ALGORITHM_KASA ])
The syntax of the LeastSquaresCircle function consists of the following parts:
Part |
Description |
||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Points |
The Y and X points for which the least squares circle is to be calculated. The same unit must be used for both components of the signal. Permitted data structures are signal. All real data types are permitted, except calendar time und time span. |
||||||||||||||||||||||||||||
Y |
The Y points used to calculate the least squares circle. If you specify a signal, then its Y component is used. The unit must match the unit of the X argument. Permitted data structures are data series und signal. All real data types are permitted, except calendar time und time span. |
||||||||||||||||||||||||||||
X |
The X points used to calculate the least squares circle. If you specify a signal, then its Y component is used. The unit must match the unit of the Y argument. Permitted data structures are data series und signal. All real data types are permitted, except calendar time und time span. |
||||||||||||||||||||||||||||
OutputOptions |
Specifies which results are to be returned. Multiple results are output as a list. If, for instance, the radius of the reference circle and the roundness should be output, the argument must contain the value LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS + LSCI_OUTPUT_ROUNDNESS. The argument OutputOptions can have the following values:
If this argument is omitted, it will be set to the default value LSCI_OUTPUT_MIDDLE_CIRCLE. |
||||||||||||||||||||||||||||
CircleSize |
Specifies the number of values used to represent the fitted circles. If you enter zero, the original number of values are retained. The argument is considered only if one of the listed circles was selected for OutputOptions. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 0. If this argument is omitted, it will be set to the default value 5000. |
||||||||||||||||||||||||||||
Algorithm |
Determines the algorithm for calculating the least squares circle. The method of least squares is always used. The argument Algorithm can have the following values:
If this argument is omitted, it will be set to the default value LSCI_ALGORITHM_KASA. |
Remarks
The values are converted to 64-bit floating points before the calculation is made.
The output options of the argument OutputOptions are visualized in the following diagram:
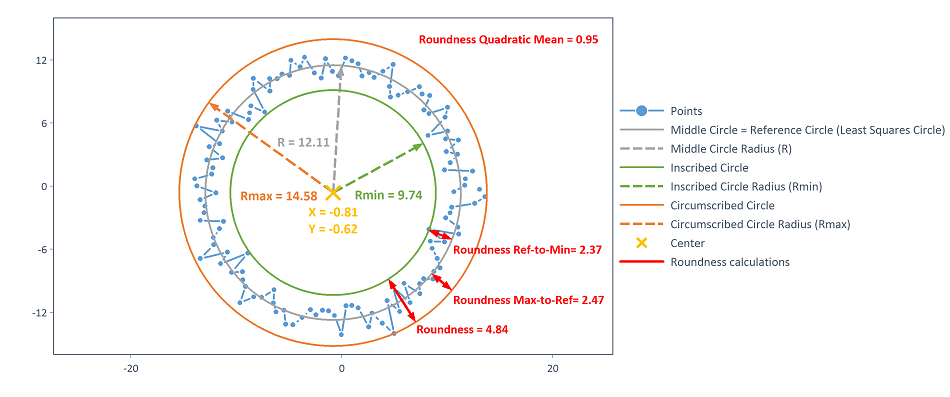
The results can be accessed using the following list element names:
Constant |
Meaning |
|---|---|
.["Center_X"] |
X coordinate of the center of the reference circle. |
.["Center_Y"] |
Y coordinate of center the reference circle. |
.["Middle_Circle"] |
Reference circle (least squares reference circle). |
.["Middle_Circle_Radius"] |
Radius of reference circle. |
.["Inscribed_Circle"] |
The largest inscribed circle related to the reference circle. |
.["Inscribed_Circle_Radius"] |
Radius of the largest inscribed circle related to the reference circle. |
.["Circumscribed_Circle"] |
The smallest circumscribed circle related to the reference circle. |
.["Circumscribed_Circle_Radius"] |
Radius of the smallest circumscribed circle related to the reference circle. |
.["Roundness"] |
Roundness deviation as the difference between the radii of the circumscribed and inscribed circles. |
.["Roundness_Max_to_Ref"] |
Peak-to-reference roundness deviation. |
.["Roundness_Ref_to_Min"] |
Reference-to-valley roundness deviation. |
.["Roundness_Quadratic_Mean"] |
Root mean square of the deviations of the data points to the reference circle. |
You can also always use the Formula.Listelementname syntax.
Note The LSCI roundness calculations are based on the currently valid standard for determining roundness; see [5].
Available in
FlexPro Professional, Developer Suite
Examples
LeastSquaresCircle(y, x)
Calculates the LSCI circle (least squares reference circle) of a point set.
LeastSquaresCircle(y, x, LSCI_OUTPUT_ROUNDNESS)
Calculates the least squares circle of a point set and returns only the roundness.
LeastSquaresCircle(points, LSCI_OUTPUT_MIDDLE_CIRCLE_RADIUS + LSCI_OUTPUT_ROUNDNESS)
Calculates the least squares circle of a point set. As the result, the radius of the reference circle and the roundness are output as a list.
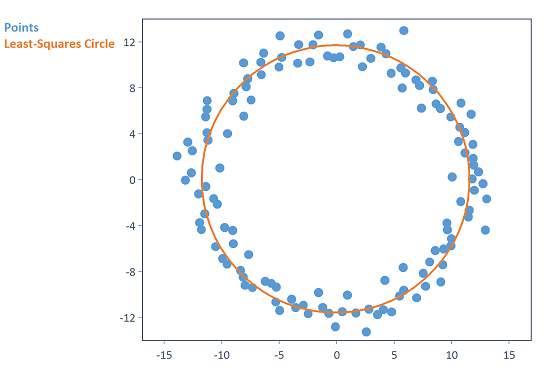
Dim alpha = Series(0, 2*PI, 0.05)
Dim r = 11.5 + Noise(1 # NumberOfRows(alpha), NOISE_NORMAL)
Dim points = Signal(Noise(1) + r*Sin(alpha), Noise(1) + r*Cos(alpha))
List("Points", points, "Least-Squares Circle", LeastSquaresCircle(points))
Calculates the least squares circle of randomly distributed points in the two-dimensional plane.
See Also
MaximumInscribedCircle Function
MinimumCircumscribedCircle Function
Circle Approximation - Analysis Object
References
[1] I. Kasa: A curve fitting procedure and its error analysis. In: IEEE Trans. Inst. Meas., Vol. 25, Pages 8-14. http://ieeexplore.ieee.org/document/6312298/,1976.
[2] L.D. Coope: Circle fitting by linear and nonlinear least squares. In: Journal of Optimization Theory and Applications, Vol. 76, Issue 2, Pages 381-388. https://link.springer.com/article/10.1007/BF00939613,1993.
[3] V. Pratt: Direct least-squares fitting of algebraic surfaces. In: Computer Graphics, Vol. 21, Pages 145-152. https://dl.acm.org/citation.cfm?id=37420,1987.
[4] A. Al-Sharadqah and N. Chernov: Error Analysis for circle fitting algorithms. In: Electron. J. Statist., Vol. 3, Pages 886-911. https://projecteuclid.org/euclid.ejs/1251119958,2009.
[5] DIN Deutsches Institut für Normung e.V.: Part 1: Vocabulary and parameters of roundness (ISO 12181-1:2011); English translation of DIN EN ISO 12181-1:2011. In: Geometrical product specifications (GPS)- Roundness. 2011.
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information