Prony Algorithm
The Prony procedure is of interest for characterizing damped sinusoids within a signal.
For real data, fitting a sum of complex exponentials is equivalent to fitting exponentially damped sinusoids. An exponentially-damped sinusoid is a sine model with a first order or exponential decay. Modified procedures fit undamped sinusoids by forcing the damping factors to zero. Several procedural modifications have been implemented to improve the Prony method's noise resistance.
The Prony algorithms are multi-step procedures:
1.Perform an AR (AutoRegressive) Fit
2.Root the AR Coefficients for Complex Exponential Parameters
3.Filter the Roots
4.Least-Squares Fit for Complex Amplitude Parameters
5.Create the Final Model with Signal Thresholding
Complex Exponential Model
A Prony model of order m consists of summing the product of a complex exponential z and a complex amplitude h.
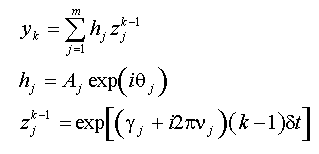
In the equations for h and z, A is the amplitude of the complex exponential, g is the damping factor, u is the frequency, and q is the phase. FlexPro reports the complex amplitudes and exponentials in the Prony procedure as real damped sinusoids:
![]()
A is the sinusoidal amplitude reported, k is the damping factor, u is the frequency, and q is the phase. Note that the model reduces to an undamped sinusoid when the damping (k) is 0 and to a first order exponential decay when the frequency (u) is 0 and the phase (q) is p/2.
AR Polynomial Roots
A complex exponential model consists of complex amplitude and exponential parameters. The estimation of the frequencies and damping factors (the exponential parameters) is done first. These values are derived from the complex roots of an AR (autoregressive) fit. When the forward prediction model is used for the damped case, the roots of the fitted AR polynomial are the complex exponential parameters in the Prony model. These complex roots yield not only the sinusoidal frequencies, but also the exponential damping factors. A forward prediction AR algorithm is employed.
SVD Algorithms
The SVD algorithms implement signal thresholding, and as such, these are likely to offer more accurate frequencies and damping factors for the components since the influence of noise can be factored out.
As with AR fits, the signal space will need to be twice the number of expected components.
Root Selection
To stabilize the Prony procedures, FlexPro implements an intermediate root filtering step. This is automatic. Negative frequency roots are removed as well as roots that appear at the Nyquist bound. The damped Prony algorithms can detect sinusoids, damped sinusoids, and real exponentials. If an AR root is at frequency 0, the function is a real exponential. If it is on the unit circle, an undamped sinusoid results. In the other instances, damped sinusoids are detected. This is strictly a function of the roots of the AR fit, and cannot be forced.
Note that real exponentials (first order exponential decays) are filtered out and do not appear in Prony models.
Complex Amplitude Least-Squares Fit
Once the roots have been identified, a linear least-squares regression is used to produce the initial estimates for the complex amplitude parameters in the model. The amplitudes and phases of the exponentially-damped sinusoids are then computed from these complex amplitudes.
Signal Thresholding
Since the Prony method fits a series of complex exponentials in a deterministic model, it is possible to truncate the signal at a specified number of components simply by discarding the least significant exponentials in the fit and to redo the complex amplitude least-squares fit with fewer components. The final Prony model thus consists of the most significant components as determined by the value set as the number of components.
Once the signal components have been paired, the complex amplitude least-squares fit is repeated using only the most significant components. This reduced component fit will be more stable and the energy spectrum smoother with lesser likelihood of spectral peaks arising from noise.
References
Excellent coverage of Prony algorithms can be found in:
•S. Lawrence Marple, Jr., "Digital Spectral Analysis with Applications", Prentice-Hall, 1987, p.303-349.
See Also
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information