GaussianFilter (FPScript)
Filters a signal with a Gaussian filter. Typically used for smoothing and as a filter for measuring and analyzing roundness.
Syntax
GaussianFilter(DataSet, Type, Fc1, [ Fc2 ], [ SamplingRate ] [ , Mode = GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION ])
The syntax of the GaussianFilter function consists of the following parts:
Part |
Description |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
The data set to be filtered. Permitted data structures are data series, data matrix, signal und signal series. All real data types are permitted, except calendar time und time span. Void values are not permitted in this argument. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||||||
Type |
Specifies the filter type. The argument Type can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
Fc1 |
Specifies the first cut-off frequency of the Gaussian filter. The frequency must be between 0 and 0.5 (half of the sampling rate normalized to one) or between 0 and 0.5 * SamplingRate. The cut-off frequency for the Gaussian filter is defined as the frequency at which the filter amplitude passes through 50 percent of the original signal amplitude. Permitted data structures are scalar value. All real data types are permitted, except calendar time und time span. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
Fc2 |
Specifies the second cut-off frequency of the Gaussian filter. The frequency must be between 0 and 0.5 (half of the sampling rate normalized to one) or between 0 and 0.5 * SamplingRate. This argument does not have to be specified for a low-pass or high-pass filter. The cut-off frequency for the Gaussian filter is defined as the frequency at which the filter amplitude passes through 50 percent of the original signal amplitude. Permitted data structures are scalar value. All real data types are permitted, except calendar time und time span. The value must be greater or equal to 0. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||
SamplingRate |
Specifies the sampling rate. The argument is optional. If the argument is not specified, then for the cut-off frequencies Fc1 and Fc2 a normalized frequency from 0 to 0.5 has to be specified in each case. Permitted data structures are scalar value. All real data types are permitted, except calendar time und time span. The value must be greater than 0. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||||||
Mode |
The filtering corresponds to the (fast) convolution with a Gaussian function in the time domain. The argument thus specifies the calculation mode for carrying out the convolution. The argument Mode can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION. |
Remarks
The Gaussian filter (low-pass) corresponds to the convolution with the following Gaussian function (convolution kernel) in the time domain:
In this equation fc stands for the cut-off frequency. The convolution in this case is calculated with the help of the FFT (fast Fourier transform) as follows: IRFFTn(FFTn(Data)*FFTn(GaussianKernel)). Since the fast Fourier transform of a Gaussian function in turn produces a Gaussian function, the transfer function (i.e. FFTn(GaussianKernel)) can be calculated explicitly. In the frequency domain, the filter is therefore calculated as multiplication with the following transfer function:
Selecting f = fc yields S(f) = 0.5, i.e. the amplitude of the filter runs through 50 percent of the original signal amplitude.
In the frequency domain, the Gaussian high-pass filter corresponds to multiplication with the transfer function 1-S(f). The bandpass and bandstop filter accordingly results as a combination of low-pass and high-pass.
For the following specific choice of fc, the Gaussian kernel is equivalently written in the time domain as convolution with a Gaussian normal distribution (with expected value of 0 and standard deviation of σ) as:
The structure of the result corresponds to that of the DataSet argument. The calculation for data matrices and signal series is made column by column. If present, the X or Z components are copied to the result unchanged.
Note The Gaussian filter can be used in particular for smoothing. It is also frequently used as a filter for measuring and analyzing roundness; see [1]. The GAUSSIANFILTERMODE_PERIODIC_BOUNDARY mode should be used when working with a periodic input data set or a closed roundness profile. In the case of non-periodic data and transient data, use the mode GAUSSIANFILTERMODE_ZERO_BOUNDARY (corresponds to zero boundary condition). For this purpose, an appropriate number of zeroes are added to the input signal for the Fourier transform (zero padding). In the case of non-periodic data with an unknown boundary condition, use the mode GAUSSIANFILTERMODE_SYMMETRIC_EXTENSION(exact boundary condition unknown, data is extended symmetrically). As a rule, this provides a natural smoothing of the edges.
Available in
Option Digital Filters
Examples
GaussianFilter(Data, FILTER_LOWPASS, 0.04)
Smooths a data set with the Gaussian low-pass filter with a cut-off frequency of 0.04. Usually produces superior smoothing compared to smoothing with a moving average using the Smooth function.
GaussianFilter(Data, FILTER_HIGHPASS, 0.01)
Removes the DC component with a Gaussian high-pass filter with a low cut-off frequency. Results are similar to those of the DCRemovalFilter function.
Dim dirac = (0 # 100) : 1 : (0 # 100)
Dim gaussCoeff = GaussianFilter(dirac, FILTER_LOWPASS, 0.04)
AmplitudeResponse(gaussCoeff)
Calculates the amplitude response of the Gaussian filter (low-pass with cut-off frequency of 0.04). The GaussianFilter function is applied to a Dirac impulse. This provides the system transfer function in the form of filter coefficients. With the help of filter coefficients, the AmplitudeResponse function can be used to calculate the filter amplitude response. The following figure shows the comparison between the amplitude response of the Gaussian low-pass filter with a cut-off frequency of 0.04 to a moving average with a smoothing width of 7 (see Smooth function). High frequencies in particular are suppressed much better than when using the moving average:
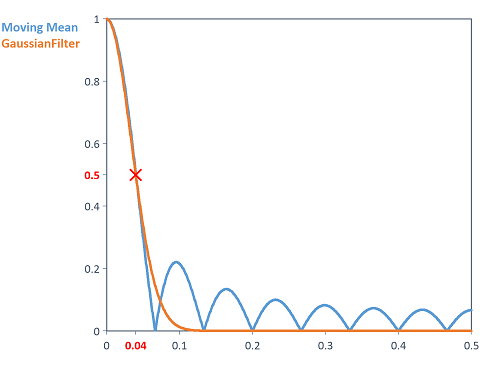
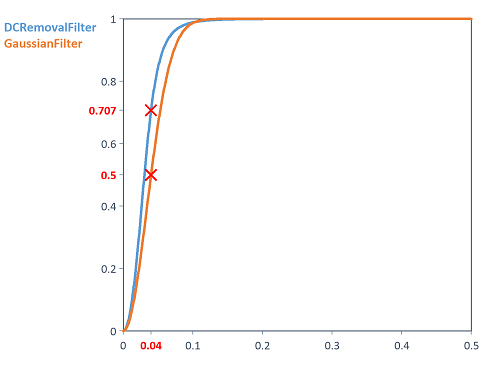
The following illustration shows the comparison between the amplitude response of the Gaussian high-pass filter with a cut-off frequency of 0.04 to the DCRemovalFilter function with the same cut-off frequency and an order of 2:
Dim sigma = 4.5
Dim fc = sqrt(log(2))/(sigma*sqrt(2)*PI)
GaussianFilter(Data, FILTER_LOWPASS, fc)
Smooths a data set through convolution with a Gaussian normal distribution with an adjustable standard deviation of σ (width).
See Also
MaximumInscribedCircle Function
MinimumCircumscribedCircle Function
Signal Smoothing Analysis Object
Circle Approximation Analysis Object
References
[1] B. Muralikrishnan, J. Raja: Computational Surface and Roundness Metrology. Springer-Verlag London Limited,2009.ISBN 1-848-00296-3.
[2] DIN Deutsches Institut für Normung e.V.: Part 2: Specification operators (ISO 12181-2:2011); English translation of DIN EN ISO 12181-2:2011-07. In: Geometrical product specifications (GPS) - Roundness. 2011.