Data Tapering Window
Data tapering windows are used to reduce spectral leakage in Fourier spectra.
Fixed Fourier Width Data Tapers
The following fixed shape data tapering windows are available in FlexPro. Window characterization takes place in the frequency domain. The dB value declares the attenuation of the first side lobe as opposed to the main lobe. The leakage decreases as the attenuation increases. The term "rolloff" describes the decay of the side lobes. The spectral spreading of the leakage decreases as the rolloff increases. The value W (Width) describes the one-sided width of the main lobe maximum as a multiple of the with of the main lobe maximum of the rectangular window. The spectral resolution decreases as the width increases.
Windows |
Calculated Using |
|---|---|
Rectangular -13dB W=1 (No Windowing) |
1.0 |
Welch -21dB W=1,4 |
1.0-(((n-1)-2*i)/(n-1)*((n-1)-2*i)/(n-1)), i=0..n-1 |
Sine -23dB W=1,5 |
sin(π*i/(n-1)), i=0..n-1 |
BiSquare -28dB W=1,8 (Connes) |
1.0-(absolute(i-0.5*n+0.5))²/(0.5*n-0.5)²)², i=0..n-1 |
Bartlett -27dB W=2 |
2*i/(n-1), i=0..(n-1)/2 2-2*i/(n-1), i=(n-1)/2+1..n-1 |
0.5-0.5*cos(2*π*i/(n-1)), i=0..n-1 |
|
TukeyHann -37dB W=2 |
0.25*Dirichlet(2*(i/(n-1))-1.0-0.5)+(1.0-2.0*0.25)*Dirichlet(2*(i/(n-1))-1.0)+0.25*Dirichlet(2*(i/(n-1))-1.0+0.5), i=0..n-1 mit Dirichlet(q)=sin((2*π+0.5)*q)/(2*π*sin(0.5*q)) |
Bartlett modifiziert -39dB W=2,3 |
(sin(π*(2*(i/(n-1))-1)))²/(2*π*sin((i/(n-1))-0.5))², i=0..n-1 |
0.53836-0.46164*cos(2*π*i/(n-1)), i=0..n-1 |
|
Cos3 Maximum Rolloff -47dB W=3 |
0.375-0.5*cos(2*π*i/(n-1))+0.125*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman -58dB W=3 |
0.42-0.5*cos(2*π*i/(n-1))+0.08*cos(4*π*i/(n-1)), i=0..n-1 |
0.44959-0.49364*cos(2*π*i/(n-1))+0.05677*cos(4*π*i/(n-1)), i=0..n-1 |
|
Cos3 Nutall -64dB W=3 |
0.40897-0.5*cos(2*π*i/(n-1))+0.09103*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman Exact -68dB W=3 |
0.42659071367153912296-0.49656061908856405847*cos(2*π*i/(n-1))+0.076848667239896818573*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Blackman-Harris -68dB W=3 |
0.42323-0.49755*cos(2*π*i/(n-1))+0.07922*cos(4*π*i/(n-1)), i=0..n-1 |
Cos3 Minimum Sidelobe -71dB W=3 |
0.4243801-0.4973406*cos(2*π*i/(n-1))+0.0782793*cos(4*π*i/(n-1)), i=0..n-1 |
Cos4 Maximum Rolloff -61dB W=4 |
0.3125-0.46875*cos(2*π*i/(n-1))+0.1875*cos(4*π*i/(n-1))-0.03125*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -74dB W=4 |
0.40217-0.49703*cos(2*π*i/(n-1))+0.09892*cos(4*π*i/(n-1))-0.00188*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -83dB W=4 |
0.338946-0.481973*cos(2*π*i/(n-1))+0.161054*cos(4*π*i/(n-1))-0.018027*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Blackman-Harris -92dB W=4 |
0.35875-0.48829*cos(2*π*i/(n-1))+0.14128*cos(4*π*i/(n-1))-0.01168*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -93dB W=4 |
0.355768-0.487396*cos(2*π*i/(n-1))+0.144232*cos(4*π*i/(n-1))-0.012604*cos(6*π*i/(n-1)), i=0..n-1 |
Cos4 Nutall -96dB W=4 |
0.3635819-0.4891775*cos(2*π*i/(n-1))+0.1365995*cos(4*π*i/(n-1))-0.0106411*cos(6*π*i/(n-1)), i=0..n-1 |
1-1.93*cos(2*π*i/(n-1))+1.29*cos(4*π*i/(n-1))-0.388*cos(6*π*i/(n-1))+0.0322*cos(8*π*i/(n-1)), i=0..n-1 |
Variable Fourier Width Data Tapers
The following adjustable shape data tapering windows are available in FlexPro:
Windows |
Calculated Using |
|---|---|
beta |
4*(1-i/(n-1))*i/(n-1))^(-3.218913776512187+2.760793796409310*a), i=0..n-1 a=width of the main lobe |
Cosine Maximum Rolloff |
absolute(0.5*(1-cos(2*p*i/(n-1)))))^(a-1), i=0..n-1 This is the cosine window with the maximum decay of the side lobes. |
Kaiser-Bessel |
I0(sqrt((a²-1.0)/0.10132118361)*sqrt(i*(2*((n-1)/2)-i))/((n-1)/2))/I0(sqrt((a²-1.0)/0.10132118361)), i=0..n-1 a=main lobe width, I0 is Modified Bessel |
van der Maas |
0.5*I1(2*(0.5*π*sqrt(4*a*a-1))*sqrt((i/(n-1))*(1-(i/(n-1)))))/(sqrt((i/(n-1))*(1-(i/(n-1))))*I1(0.5*π*sqrt(4*a*a-1))), i=0..n-1 a=main lobe width, I1 is Modified Bessel |
This window produces the minimum side lobe leakage, but offers zero rolloff. It is constructed in the frequency domain and inverted to produce the time domain data) FlexPro implements the Chebychev window in a range from -30 dB to -150 dB.
See program 5.2 in "IEEE Programs for Digital Signal Processing" |
|
Chebyshev (approximated) |
This is an FlexPro approximation to the Chebshev window that is valid between -50 and -130 dB. It is mainly used in the Unevenly Spaced Data Fourier Analysis analysis object. |
Slepian (DPSS) |
This is the first of the Slepian discrete prolate spheroidal sequences, or eigentapers, with a equal to approximately the main lobe width.
See Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis" |
Gaussian |
exp(-4*ln(2)*((i-((n-1)/2))/((n-1)*((2.453274901281656+a*0.3202556336455866)/(1.0+a*(2.348619671799226))))²), i=0..n-1 a=width of the main lobe |
Cosine Taper |
if(i>(int)(a*n+0.5) and i<(int)((1.0-a)*n-0.5)), 1.0, 0.5-0.5*cos((π/a/(n-1))*(if(i>0.5*n, n-i-1, i)))), i=0..n-1 Taper ranges from Hann with a=0.5 to rectangular as a approaches 0. |
The following graphs show a number of popular windows:
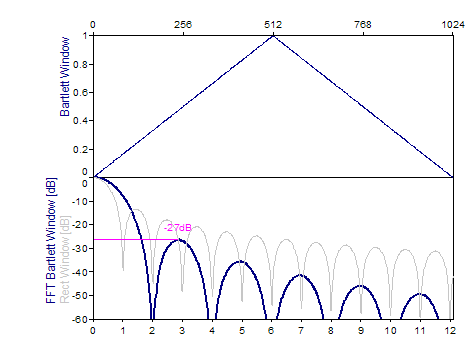
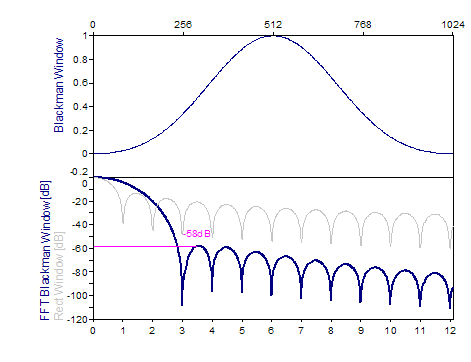
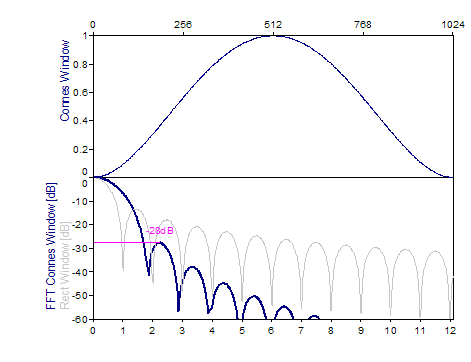
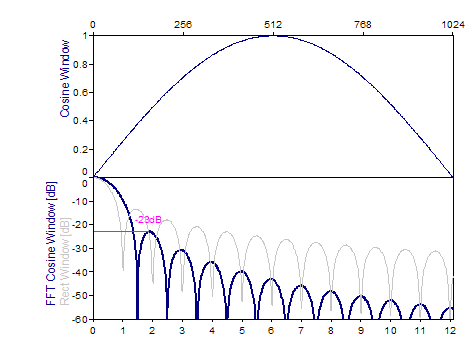
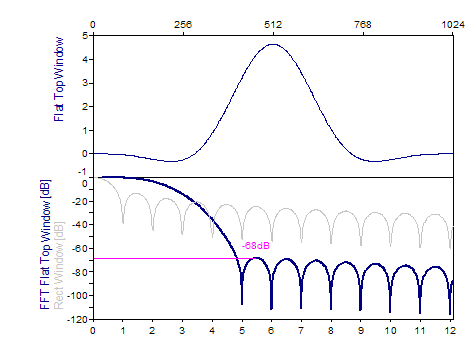
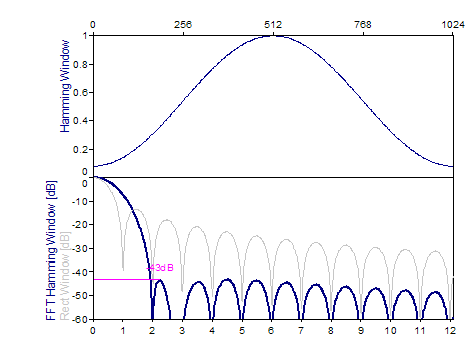
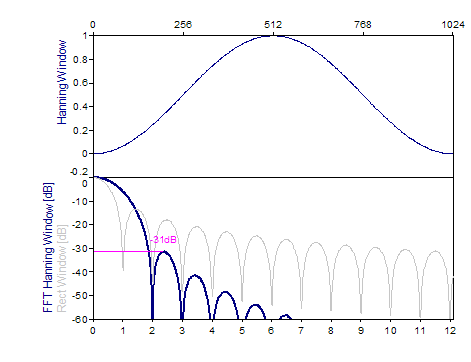
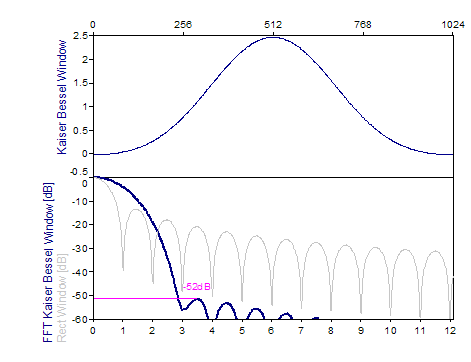
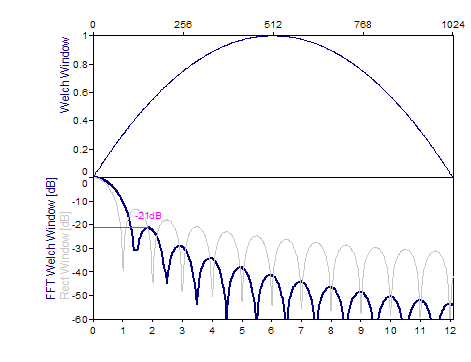
References
An implementation of the Chebyshev window is described in:
•IEEE Programs for Digital Signal Processing, IEEE Press, 1979. FlexPro offers the Chebyshev window from -30dB to -150dB.
The Slepian (DPSS) Window is described in:
•Jonathan Lees and Jeffrey Park, "Multiple Taper Spectral Analysis", Computers and Geosciences, v21, p199, 1995.
The following reference may be of interest:
•Albert H. Nuttall, "Some Windows with Very Good Sidelobe Behavior", IEEE Trans. ASSP, v29-1, Feb. 1981.