The disadvantage to designing FIR filters using the window method is that the approximation error cannot be influenced in different frequency ranges. It is therefore often better when designing filters to implement the minimax strategy (minimize the maximum error) or an error criterion with weighting of the frequency. This results in the "best" filter that can be achieved for a defined specification.

The FIR Equiripple method, which is also known as Remez Exchange method, Parks-McClellan, always provides the FIR filter with minimum effort. The Parks-McClellan method provides the solution for the FIR filter using the Remez Exchange algorithm in an iteration process. Since filters can be designed using this approximation method with a constant ripple both in the passband and stopband, the filter is also known as the equiripple filter.

The Remez Exchange algorithm is an optimizing algorithm based on Chebyshev polynomials. An error function is formed for the desired filter from a linear combination from cosine functions and is minimized by an efficient optimization process.

Minimax or Chebyshev Criterion

The Chebyshev or Minimax Criterion is used for this design method. For this method, a search is performed in fixed frequency intervals for a frequency response A(ejω) that minimizes the maximum weighted approximation error of the error function. The following error function is generated for this:

E(ω)    …  error function

W(ω)   …  weighting function

H(ejω) …  desired frequency response

A(ejω) …  approximation function

The error function, weighting function and the desired frequency response are defined only for closed partial intervals of the normalized frequency range 0 <= ω <= 0.5. For instance, a low pass filter has the intervals 0 <= ω <= ωp   and ωs <= ω <= 0.5. The approximation function is not limited within the transition width and can therefore take any shape, since no error limits are defined here.

Filters for freely defined frequency responses can be designed. To do this, you can pass the desired frequency response as a signal whose Y component contains the amplitudes as a continuous curve and whose X component contains the associated normalized frequencies (range of 0 - 0.5).

Principle of the Remez Exchange Algorithm

The procedure is based on reformulation of the filter design task into a task for polynomial approximation. Using an iteration procedure, a clear polynomial function pn  (x) is approximated, which fulfills the defaults pn  (xi)=yi±h within an error band ±h. The polynomial oscillates within the error band in the local extrema by ±h. You can choose the polynomial degree n and the error band ±h. To do this, the alternation theorem is applied, which is explained in detail in Oppenheim and Schafer and other works.

1. Determine the least squares fitting polynomial pn  (x) from the degree n for an amount of n+2 data points (xi, yi) by solving the linear equation system for the polynomial coefficients a0..an  and the error h. The function values yi (i=1..n+2) to be achieved are predefined. You therefore obtain an equation system with n+2 equations:

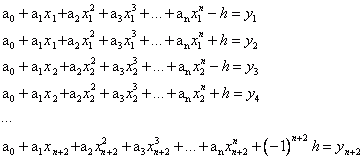
2. Determine the n+2 extrema of deviations from the default.

3. Determine the new least squares fitting polynomial from the degree n by using new values xi, which are at the extrema, as in 1.

4. Repeat algorithm until the error ±h is sufficient for the defaults.

The procedure is very flexible and can be used to achieve optimal solutions for most non-recursive filters (e.g. low pass, high pass, bandpass and multiband filters with piecewise-constant amplitude response, digital differentiations and Hilbert transformations). It is even possible to predefine any amplitude response and determine the optimal filter from this.

One of the most popular computer algorithms based on the Remez Exchange algorithm is from James H. McClellan, Thomas W. Parks and Lawrence R. Rabiner and is also known as the Parks-McClellan method. The algorithm used in FlexPro is based on this algorithm. With this algorithm, you can design filters with predefined filter lengths and determine optimal filters with a predefined specification.

Weighting of Errors and Error Limits

There are two options for calculating an FIR filter. Either you can specify the filter length or you can pre-define a specification and calculate the length of the filter from this.

Predefined Filter Length

If the filter length is specified, only the ratio of errors of individual bands can be defined, since there is no assurance as to whether the desired specification (absolute error limits) can be preserved using the specified filter length.

The predefined filter length corresponds to the length of the impulse response. In this case, the weighting of the errors of the individual bands is specified. The weighting factors are in relation to one another. For a multiband filter with three bands, the weighting information {1, 10, 1} means, for instance, that the second band has one ripple that is ten times lower than the other two bands. This range is thus smoother. If the weighting is not specified, all bands will have the same weighting ratio.

Predefined Specification

The filter length is not specified in this case. Instead, all desired error limits are specified. Using this information, the filter length L is empirically estimated using the following formula:

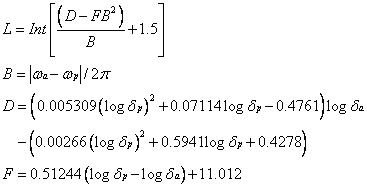
[Quelle: Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York, p. 701]

This formula applies only to low pass and high pass filters. For multiband filters, the filter length is calculated for each transition from one band to the next. The largest value is taken as the starting value. Next, the filter length is increased or reduced until the optimal filter has been determined for the desired specification.

The procedure can only be solved numerically and therefore it is a relatively intensive procedure for higher orders. However, it is an optimal solution as opposed to the window method. It is possible, however, that the algorithm may find no solution due to problems with convergence.

References

•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.

•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.

•J. H. McClellan, T. W. Parks, L. R. Rabiner. A Computer Program for Designing Optimum FIR Linear Phase Digital Filters. IEEE Transactions on Audio and Electroacoustics, Vol. AU-21, No.6, December 1973

•L. R. Rabiner, J. H. McClellan and T. W. Parks. FIR Digital Filter Design Techniques Using Chebyshev Approximation. Proceedings IEEE, Vol. 63, No. 4, pp. 595 610, April 1975