FIRFilterEquiripple (FPScript)
Calculates the impulse response of an FIR band filter using the equiripple algorithm.
Syntax
FIRFilterEquiripple(NumberOfBands, BandEdges, GainFactor, WeightingOfErrors, [ FilterLength ] [ , SamplingRate ])
The syntax of the FIRFilterEquiripple function consists of the following parts:
Part |
Description |
|---|---|
NumberOfBands |
Specifies the number of bands. The number of bands must be between 1 and 40. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater or equal to 1 and less or equal to 40. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
BandEdges |
Specifies the lower and upper band limits. The frequencies are between 0 and half the sampling rates or, with normalized frequencies, between 0 and 0.5. Permitted data structures are data matrix. All real data types are permitted, except calendar time und time span. Void values are not permitted in this argument. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
GainFactor |
Specifies the amplitudes of the bands. 1 defines a bandpass and 0 defines a bandstop. Permitted data structures are data matrix und signal. All real data types are permitted, except calendar time und time span. Void values are not permitted in this argument. For the X component additional restrictions do apply.Void values are not permitted in this argument. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
WeightingOfErrors |
A data series or a signal with weighting of errors when the filter length is specified, or a data series with the maximum approximation errors for the individual bands. Permitted data structures are data series und signal. All real data types are permitted, except calendar time und time span. Void values are not permitted in this argument. For the X component additional restrictions do apply.Void values are not permitted in this argument. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
FilterLength |
Specifies the filter length. The argument is optional. Permitted data structures are scalar value. All integral data types are permitted. The value must be greater than 4 and less than 1000. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
SamplingRate |
Specifies the sampling rate. The argument is optional. If a sampling rate is specified, the absolute cut-off frequencies are specified for the cut-off frequencies instead of normalized frequencies. Permitted data structures are scalar value. All real data types are permitted, except calendar time und time span. The value must be greater than 0. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
Remarks
The filter coefficients are returned as data series. Use the Filter function to filter data with the calculated filter coefficients.
The argument BandEdges is a data matrix with n data series, each with two 64-bit floating point values, where n is the number of bands. The first value of a data series specifies the lower band limit and the second value specifies the upper band limit. The values must be in ascending order and the transition width between two bands must be greater than 0.
The argument GainFactor can be a data matrix with n (n = number of bands) data series, each with two 64-bit floating point values, or a signal. 1 defines a bandpass and 0 defines a bandstop. If the gain factor is a matrix, the values are assigned to the band limits. The amplitude response of the bands is determined from this. If a signal is specified, any amplitude response can be provided. The Y component contains the amplitude and the X values contain the associated frequencies from 0 to half the sampling rate or from 0 to 0.5. In this case, however, only the frequency ranges are used that are defined in the list with the frequency bands.
The argument WeightingOfErrors can be a data series with n 64-bit floating point values or a signal. If the filter length is specified, then error weighting can be provided here, which is the ratio between the error limits of the individual bands. If no filter length is specified, then the absolute error limits for the individual bands are specified and the optimal filter length is determined from this. A higher frequency band weighting compared to another frequency band means that the error limit is lower, which means there is less ripple. With a specified filter length, the weighting can also be specified as a signal, where the X component contains the frequencies 0 to half the sampling rate or 0 to 0.5. If both the gain factor and weighting are specified as a signal, then both signals must contain the same X values.
Note An increase in order / filter length causes the filter to be steeper and reduces the ripple.
Available in
Option Digital Filters
Examples
FIRFilterEquiripple(3, {{0, 0.1},{0.12, 0.2},{0.22, 0.5}}, {{0, 0},{1, 1},{0, 0}}, {0.05, 0.01, 0.1})
The following illustration shows the frequency response of the calculated multiband FIR filter. This involves three bands (stop-band, pass-band, stop-band) with frequency ranges from 0 to 0.1, 0.12 to 0.2 and 0.22 to 0.5. The maximum error is 0.05 for the first band, 0.01 for the second band, and 0.1 for the third band.
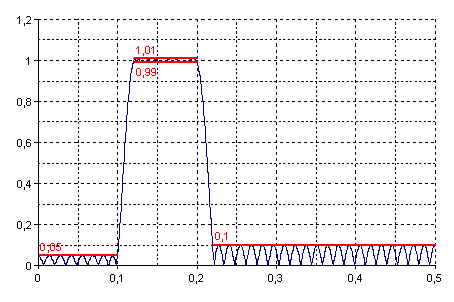
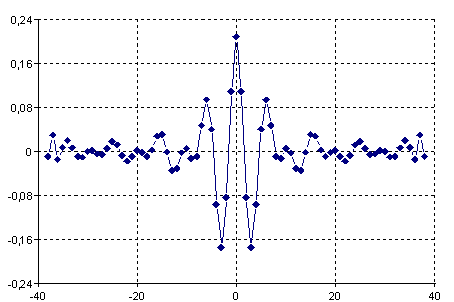
Using the predefined specification, the function determines an FIR filter with a length of 77 with the following impulse response:
The following illustration shows a chirp sine filtered using the designed filter:
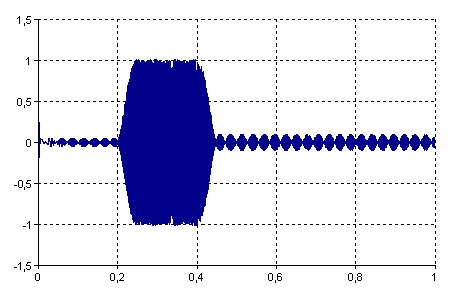
Filter(Signal, FIRFilterEquiripple(3, {{0 Hz, 100 Hz},{120 Hz, 200 Hz},{220 Hz, 500 Hz}}, {{0, 0},{1, 1},{0, 0}}, {0.05, 0.01, 0.1}, , SamplingRate(Signal)), , TRUE)
The function filters a signal with phase correction using the filter calculated in the first example. Note that the second argument of the filter function is left empty.