Filter (FPScript)
Filters a data set with a Finite Impulse Response (FIR) or an Infinite Impulse Response (IIR) filter.
Syntax
Filter(DataSet, b, [ a ] [ , PhaseCorrection = FALSE ])
or
Filter(DataSet, FilterCoefficients [ , PhaseCorrection = FALSE ])
The syntax of the Filter function consists of the following parts:
Part |
Description |
|---|---|
DataSet |
The data set to be filtered. Permitted data structures are data series, data matrix, signal und signal series. All numeric data types are permitted. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
b |
A data series with numerator coefficients of the filter's transfer function. Alternatively, in the case of an IIR filter, a three-row matrix with the coefficients of the numerators of a cascade of 2nd order filters can be specified. Permitted data structures are data series, data matrix und list. All numeric data types are permitted, except calendar time und time span. |
a |
A data series with denominator coefficients of the filter’s transfer function. Alternatively, a three-row matrix with the coefficients of the denominators of a cascade of 2nd order filters can be used. Permitted data structures are data series, data matrix und list. All numeric data types are permitted, except calendar time und time span. |
FilterCoefficients |
A list with numerator and denominator coefficients of the filter's transfer function. You should name the list elements "b" and "a". These can be presented as a data series or as a three-row data matrix for the coefficients of a cascade of 2nd order filters. If you do not specify a name, the first list element will be used as "a" and the second will be used as "b". If DataSet is a list, then you have the option of passing this argument as a list of lists. Permitted data structures are list. All numeric data types are permitted, except calendar time und time span. |
PhaseCorrection |
The value TRUE specifies that phase correction will take place after filtering. Infinite impulse response (IIR) filters are filtered twice in this case: once forward and once backward. With finite impulse response (FIR) filters, phase correction takes place using the formula t = T/2 (L - 1) if the filter is uneven or t = LT/2 if the filter is even (L = filter length). Phase correction is only available with the Digital Filters option license. Permitted data structures are scalar value. Supported data types are Boolean value. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value FALSE. |
Remarks
The result has the same structure and unit as the argument DataSet.
Before filtering, the values are converted into real or complex 64-bit floating point values. The data type of the result is always a real or complex 64-bit floating point value. If the denominator coefficients a are specified, the first value of this data series should equal one, or in each case the first row of a three-row matrix (if a cascaded display) should be equal to one. If this is not the case, then the filter coefficients are normalized using the specified value. The first value of a cannot be zero. In the case of a cascaded display, the first row of all columns of the three-row matrix must not contain a zero. The function implements the filter as an LTI system with "transposed direct form II" according to the following block diagram:

The structure corresponds to the following system of differential equations:
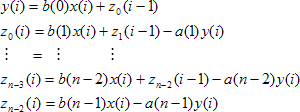
Available in
FlexPro Basic, Professional, Developer Suite
Examples
Filter(Signal, 0.25 # 4) |
Smooths a signal with a moving average with a smoothing width of 4. |
Filter(Signal, [<b> {-0.245, -0.245}, <a> {-1, 0.509} ]) |
Carries out low-pass filtering with a single-pole IIR filter. |
See Also
FIR Filter Analysis Object (Equiripple Method)
FIR Filter Analysis Object (Window Method)
References
[1] "Oppenheim, A. V. and Schafer, R. W.": "Discrete-Time Signal Processing, 2nd Edition". "Prentice Hall, New Jersey",1999.ISBN 0-13-754920-2.
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information