Convolution Analysis Object *
You can use this analysis object to calculate the convolution product of two data sets.
For the circular convolution product the calculation occurs with the assumption that one or more complete periods of a periodic signal are saved in both data sets. For these variations, both data sets must have the same number of values. The result therefore also has this number of values. If one of the arguments has an X component, this also applies to the result. This component then contains the time lag τ of the convolution.
The non-circular convolution product is based on the assumption that the signals outside of the section specified by the data sets amount to zero. A sufficient number of zeros are therefore appended to both data sets before the transitioning to the frequency domain. If one of the arguments has an X component, this also applies to the result. This component then contains the time lag τ of the convolution. The convolution product is calculated for all τ values for which the convolution can have a value not equal to zero, i.e., for which there is still an overlap of both signals.
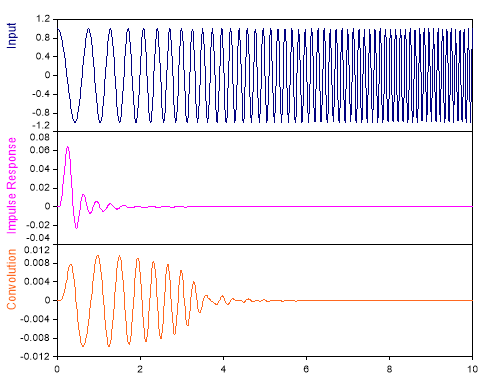
The following illustration shows an application of the convolution integral. This is a low-pass filter in the time domain. The signal is convoluted with the impulse response from a low-pass filter:
FPScript Functions Used
See Also
* This analysis object is not available in FlexPro View.
You might be interested in these articles
You are currently viewing a placeholder content from Facebook. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou need to load content from reCAPTCHA to submit the form. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from Instagram. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More InformationYou are currently viewing a placeholder content from X. To access the actual content, click the button below. Please note that doing so will share data with third-party providers.
More Information