Convolution (FPScript)
Calculates the convolution product of two signals.
Syntax
Convolution(Signal1, Signal2 [ , Mode = CONVOLUTION_NONCIRCULAR ])
The syntax of the Convolution function consists of the following parts:
Part |
Description |
||||||
|---|---|---|---|---|---|---|---|
Signal1 |
The signal that is convoluted with the second signal. Permitted data structures are data series, data matrix, signal und signal series. All numeric data types are permitted. Void values are not permitted in this argument. For the X component additional restrictions do apply.The values must have a constant positive spacing. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
Signal2 |
The signal that is convoluted with the first signal. Permitted data structures are data series, data matrix, signal und signal series. All numeric data types are permitted. Void values are not permitted in this argument. For the X component additional restrictions do apply.The values must have a constant positive spacing. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||
Mode |
Specifies the calculation mode. The argument Mode can have the following values:
If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. If this argument is omitted, it will be set to the default value CONVOLUTION_NONCIRCULAR. |
Remarks
The result always has the data type 64-bit floating point.
The unit of the result is the same as the product of the units of Signal1 and Signal2. The convolution product for two data series s and g is defined as:
and N, the number of values in s and g.
The calculation occurs in the frequency domain in all cases according to the following formula:
IRFFTn(*FFTn(Signal1) * FFTn(Signal2 ))
For two-dimensional arguments, the calculation is carried out column by column, and the result is also two-dimensional. If one of the arguments has an X component, this also applies to the result. This component then contains the time lag τ of the convolution product. Note: If the other argument does not have an X component, the same sampling is used for this argument as is used for the argument with the X component.
For circular convolution, the calculation takes place with the assumption that one or more complete periods of the signals to be analyzed are stored in Signal1 and Signal2. In this case, the number of rows of Signal1 and Signal2 must match.
The non-circular convolution is based on the assumption that the signals outside of the sections covered by the Signal1 and Signal2 data sets amount to zero. A sufficient number of zeros are therefore appended to the data sets before the transform into the frequency domain. The convolution product is calculated for all τ values for which the convolution can have a value not equal to zero, i.e., for which there is still an overlap of both signals.
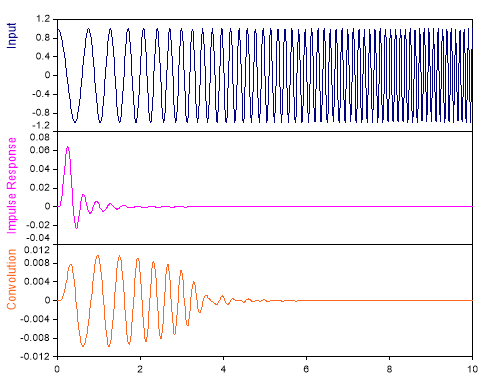
The following illustration shows the convolution of a swept-frequency cosine signal with the impulse response of a low-pass filter for all positive τvalues:
Available in
FlexPro Basic, Professional, Developer Suite
Examples
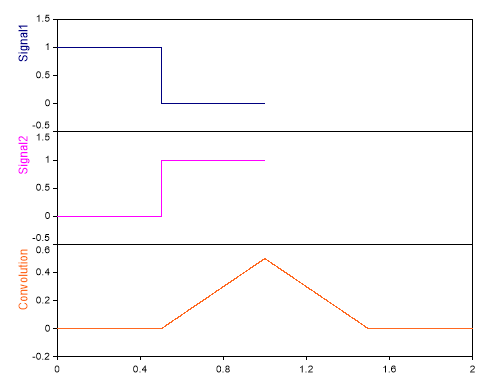
Dim Signal1 = Signal(0.5 * Square(2. * PI * 1.0 * (1000, 0.0, 0.001), 0.5) + 0.5, (1000, 0.0, 0.001))
Dim Signal2 = Signal(0.5 * Square(2. * PI * 1.0 * ((1000, 0.0, 0.001) + 0.5), 0.5) + 0.5, (1000, 0.0, 0.001))
Convolution(Signal1, Signal2, CONVOLUTION_NONCIRCULAR)
Non-circular convolution product of two rectangular signals.
See Also
References
[1] "Oppenheim, A. V. and Schafer, R. W.": "Discrete-Time Signal Processing, 2nd Edition", page 570 - 73. "Prentice Hall, New Jersey",1999.ISBN 0-13-754920-2.
[2] "H. D. Lüke": "Signalübertragung (Signal Transmission)", page 79 - 81. "Springer-Verlag Berlin, Heidelberg, New York",1985.ISBN 3-540-15526-0.