Approximation (FPScript)
Approximates a linear model Y(X) to given data according to the method of the least square error.
Syntax
Approximation(DataSet, Model)
or
Approximation(Amplitude, Time, Model)
The syntax of the Approximation function consists of the following parts:
Part |
Description |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
The signal or data series for which the approximation is to be calculated. If you specify a data series, then the X component will be generated automatically. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the function is executed for each element of the list and the result is also a list. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Amplitude |
A data series with the Y component of a signal. If you specify a signal, then its Y component is used. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Time |
A data series with the X component of a signal. If you specify a signal, then its Y component is used. Permitted data structures are data series und signal. All numeric data types are permitted. For complex data types the absolute value is formed. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Model |
Specifies the composition of the model function for which the coefficients are determined by the approximation. You can specify custom or predefined element functions.
The custom model function is passed as a data series of strings. For instance, the model function Y = A + B * X + C * sin(2 * PI * X) is described by the data series {"1", "X", "sin(2*PI*X)"}.
The model function with predefined element functions can be formed by adding the following values. For example, if the desired model function is A + B * X + C * X2, then the Model argument must receive the value APPROX_C + APPROX_X + APPROX_X_2. Approximation then calculates the unknown coefficients A, B and C so that the model function approximates the specified signal as best as possible.
Permitted data structures are scalar value und data series. Supported data types are 16-bit integer, 32-bit integer und string. If the argument is a list, then the first element in the list is taken. If this is also a list, then the process is repeated. |
Remarks
As the result the function returns a data series of data type 64-bit floating point.
The number of values equals to the number of element functions of the model function plus one.
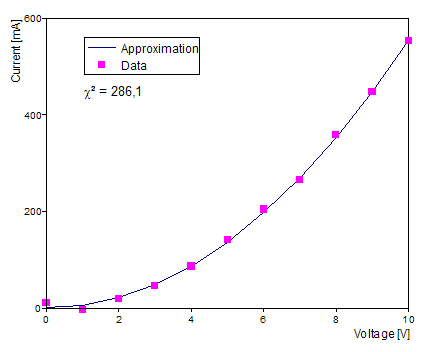
The last value represents the goodness-of-fit measure Χ2 (Chi-square). This is the sum of the squares of all deviations of the approximated model function from the data. The smaller Χ2 is, the better the found model function approximates the data. The other values of the data series return the coefficients of the element functions used in the model function, where the order corresponds to the order in the table above.
The following illustration shows measured data of a quadratic characteristic curve and its approximation:
Available in
FlexPro Basic, Professional, Developer Suite
Examples
Dim _c = Approximation(Signal, APPROX_C + APPROX_X + APPROX_X_2)
Signal(_c[0] + _c[1] * (Signal.X) + _c[2] * (Signal.X)^2., Signal.X)
Approximates a signal with a quadratic model function.
Dim _c = Approximation(Signal, {"1", "sin(2*PI*X)"})
Signal(_c[0] + _c[1] * sin(2 * PI * Signal.X), Signal.X)
Approximates a signal with a custom model function Y(X) = A + B * Sin(2*PI*X).
See Also
2D Approximation Analysis Object
References
[1] "Philip R. Bevington, D. Keith Robinson": "Data Reduction and Error Analysis for the Physical Sciences, 3rd Edition". "McGraw-Hill, New York",2003.ISBN 0-07-247227-8.
