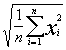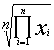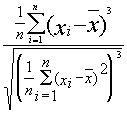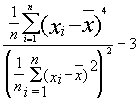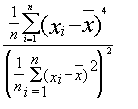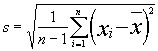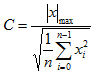weisang.com > Dokumentation > Analyseobjekt Statistische Kenngröße

FlexPro-Dokumentation

Analyseobjekt Statistische Kenngröße

09.03.2021

Mit diesem Analyseobjekt berechnen Sie verschiedene statistische Kenngrößen eines Datensatzes.

Die Berechnung einer statistischen Kenngröße führt von einer Stichprobe (Datenreihe) auf einen skalaren Wert, der eine bestimmte Eigenschaft der Stichprobe beschreibt. Extrema, Mittelwerte und Quantile können, basierend auf einer gegebenen Intervallbreite, auch blockweise oder gleitend berechnet werden. Bei der blockweisen Berechnung enthält das Ergebnis einen Wert pro Intervall. Bei der gleitenden Berechnung bleibt die Werteanzahl erhalten und für jeden Wert wird der durch die Intervallbreite bestimmte Bereich um diesen Wert berücksichtigt.

Sämtliche Kenngrößen können für alle Datenstrukturen außer Einzelwerten ermittelt werden. Bei Datenreihen ist das Ergebnis ein Einzelwert sofern keine gleitende oder blockweise Berechnung gewählt wurde. Bei Datenmatrizen können Sie statistische Kenngrößen entweder zu deren Spalten oder Zeilen oder global für den gesamten Datensatz berechnen. Wenn Sie die Option Kenngrößen für Spalten wählen, wird je eine Kenngröße für jede einzelne Spalte (Datenreihe) in der Datenmatrix berechnet. Als Ergebnis erhalten Sie dann eine Datenreihe, deren Werteanzahl der Anzahl der Spalten (Datenreihen) in der Datenmatrix entspricht. Wenn Sie die Option Kenngrößen für Zeilen wählen, wird je eine Kenngröße zu jeder Zeile berechnet. Als Ergebnis erhalten Sie dann eine Datenreihe, deren Werteanzahl der Anzahl der Zeilen in der Datenmatrix entspricht. Die Option Spalten vorher mitteln wandelt die Matrix vor der Berechnung der Kenngröße durch arithmetische Mittelung in eine Datenreihe und die Option Spalten vorher verketten hängt die Spalten zu einer langen Datenreihe aneinander. Das Ergebnis entspricht dann jenem, dass man für eine entsprechende Datenreihe erhielte. Verwenden Sie die Option Spalten vorher verketten z. B., um das globale Maximum einer Signalreihe zu ermitteln.

Bei den zusammengesetzten Datenstrukturen Signal, Signalreihe und Raumkurve wird nur die Y-Komponente betrachtet. Bei der Berechnung einer gleitenden Kenngröße werden die X- und Z-Komponente unverändert in das Ergebnis kopiert. Wird eine Blockkenngröße berechnet, dann werden die Daten der Z- oder Z-Komponente, in Abhängigkeit von der Berechnungsrichtung, dezimiert, indem der jeweils erste Wert eines Blockes in das Ergebnis übernommen wird.

Summen *

Kenngröße	Formel	Bemerkung
Summe		Summe der Daten
Quadratsumme		Summe der Quadrate der Daten

Extremwerte

Kenngröße	Formel	Bemerkung
Minimum		Kleinster Wert
Maximum		Größter Wert

Mittelwerte

Kenngröße	Formel	Bemerkung
Arithmetischer Mittelwert		Durchschnittswert
Quadratischer Mittelwert (Effektivwert)		Gibt die Amplitude an, die ein konstantes Signal gleicher Leistung hätte.
Geometrischer Mittelwert *		Zu verwenden, wenn die Werte relative Größen sind (multiplikativ). Entspricht dem arithmetischen Mittelwert bei logarithmischer Skalierung.
Harmonischer Mittelwert *

Momente *

Kenngröße	Formel	Bemerkung
Schiefe		Maß für die Symmetrie einer Verteilung. Werte kleiner bzw. größer Null geben an, dass die Verteilung links- bzw. rechtsschief ist. Die Schiefe ist Null für eine symmetrische Verteilung.
Exzess		Der Exzess gibt die Differenz der Wölbung der betrachteten Funktion zur Wölbung der Dichtefunktion einer normalverteilten Zufallsgröße an. Werte größer bzw. kleiner Null geben an, dass das absolute Maximum der Verteilung größer bzw. kleiner als das der zugeordneten Normalverteilung (mit gleicher Varianz) ist.
Wölbung		Die Wölbung oder Kurtosis ist eine Maßzahl für die Steilheit bzw. „Spitzigkeit“ einer Verteilung.

Kenngröße

Formel

Bemerkung

Schiefe

Maß für die Symmetrie einer Verteilung. Werte kleiner bzw. größer Null geben an, dass die Verteilung links- bzw. rechtsschief ist.

Die Schiefe ist Null für eine symmetrische Verteilung.

Exzess

Der Exzess gibt die Differenz der Wölbung der betrachteten Funktion zur Wölbung der Dichtefunktion einer normalverteilten Zufallsgröße an. Werte größer bzw. kleiner Null geben an, dass das absolute Maximum der Verteilung größer bzw. kleiner als das der zugeordneten Normalverteilung (mit gleicher Varianz) ist.

Wölbung

Die Wölbung oder Kurtosis ist eine Maßzahl für die Steilheit bzw. „Spitzigkeit“ einer Verteilung.

Quantile *

Zur Berechnung des Quantils werden die Daten aufsteigend sortiert, und dann der Wert an der Position n / α entnommen. Wenn n / α keine ganze Zahl ist, wird zwischen den beiden benachbarten Werten linear interpoliert.

Kenngröße	Formel	Bemerkung
Unteres Quartil
Median
Oberes Quartil

Streuungsmaße (Dispersionsmaße) *

Kenngröße	Formel	Bemerkung
Spannweite		Spannweite zwischen größtem und kleinstem Wert.
Standardabweichung		Wurzel aus der Varianz.
Varianz		Quadratisches Streuungsmaß, bezogen auf das arithmetische Mittel.
Mittlerer Quadratischer Fehler		Wie die Varianz, jedoch auf die komplette Werteanzahl bezogen.
Quartilsabstand		Differenz zwischen oberem und unterem Quartil.
Absoluter Variationskoeffizient		Standardabweichung, bezogen auf den Mittelwert.
Relativer Variationskoeffizient		Variationskoeffizient, bezogen auf sein absolutes Maximum.
Mittlere absolute Abweichung vom Median
Mittlere absolute Abweichung vom Mittelwert
Scheitelfaktor (Crest-Faktor)		Spitzenwert, bezogen auf den Effektivwert.
Quartilsdispersionskoeffizient