Analyseobjekt Signalskalierung *
Mit diesem Analyseobjekt können Sie einen Datensatz linear oder mittels einer Kennlinie transformieren. Sie können einen der folgenden Modi wählen:
Auswahl |
Bedeutung |
|---|---|
Keine Skalierung |
Die Daten werden unverändert ins Ergebnis kopiert. Wählen Sie diesen Modus, wenn Sie nur einen Trend entfernen möchten. |
Skalierung über Steigung und Achsenabschnitt |
Lineare Skalierung gemäß: Steigung * Daten + Achsenabschnitt
|
Skalierung über zwei Punkte |
Lineare Skalierung gemäß: Y1 + (Y2 - Y1) / (X2 - X1) * (Daten - X1) Mit den beiden Punkten X1, Y1 und X2, Y2. |
Einpunktkalibrierung |
Korrigiert einen Verstärkungsfehler in der Messkette. Der Kalibrierwert ist der Sollwert, mit dem das Messsystem beaufschlagt wurde. Dieser sollte möglichst am oberen Ende des Dynamikbereichs der Messekette liegen. Die Kalibriermessung ist eine Zeitreihe oder ein Einzelwert mit dem gemessenen Istwert. Wird eine Zeitreihe angegeben, wird diese automatisch gemittelt, um den Istwert zu erhalten. Die Daten werden gemäß folgender Abbildung linear transformiert: Kalibrierwert / Kalibiermessung * Daten |
Zweipunktkalibrierung |
Korrigiert einen Verstärkungs- und einen Nullpunktfehler in der Messkette. Die beiden Kalibrierwerte sollten so gewählt werden, dass möglichst der komplette Dynamikbereich der Messkette überspannt wird. Die Daten werden gemäß folgender Abbildung linear transformiert: Y = Kalibrierwert1 + (Kalibrierwert2 - Kalibrierwert1) / (Kalibriermessung2 - Kalibriermessung1) * (Daten - Kalibriermessung1) |
Kennlinientransformation |
Abtastung gemäß: Sample(Kennlinie, Daten, TRUE) Die Kennlinie wird als Datensatz mit der Datenstruktur Signal angegeben. Die Y-Komponente enthält die Sollwerte und die X-Komponente die zugehörigen Istwerte. Die X-Komponente der Kennlinie sollte einen Wertebereich umfassen, der den Wertebereich der zu skalierenden Daten vollständig umschließt. Ansonsten wird an den Rändern der Kennlinie linear extrapoliert. |
Bei zusammengesetzten Datenstrukturen, z. B. einem Signal, werden nur die Y-Werte skaliert und die X-Werte unverändert ins Ergebnis übernommen.
Einen eventuell vorliegenden Trend können Sie zuvor aus den Daten entfernen.
Auswahl |
Bedeutung |
|---|---|
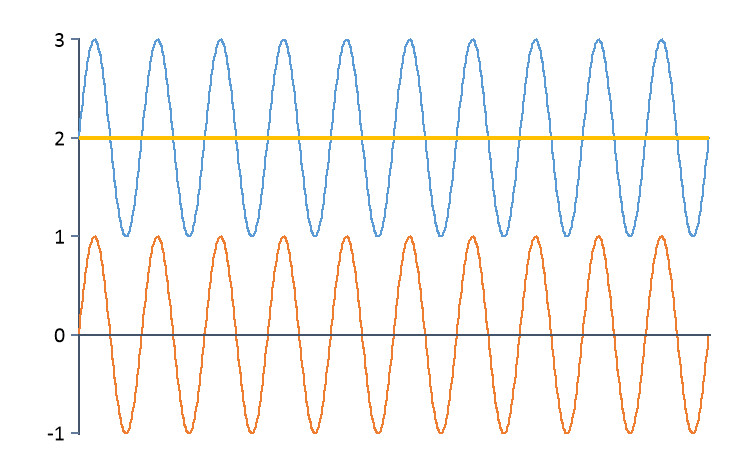
Konstant |
Subtrahiert den Mittelwert des Datensatzes.
|
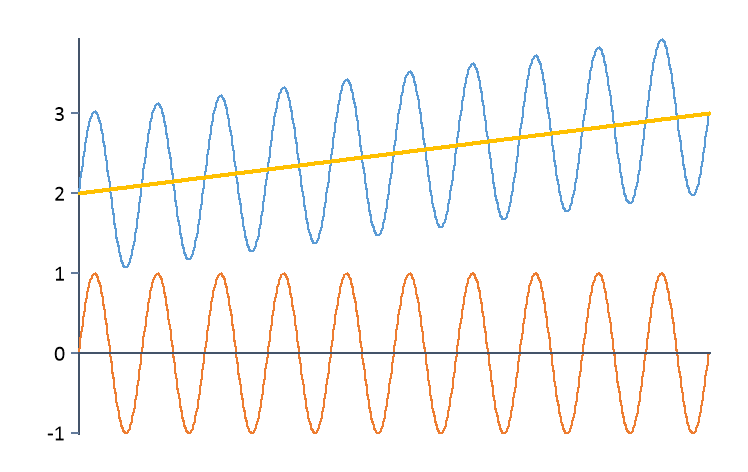
Linear |
Subtrahiert die Bestgerade, d. h. die Gerade für die die Summe der Quadrate der Abweichungen zum Datensatz minimal ist.
|
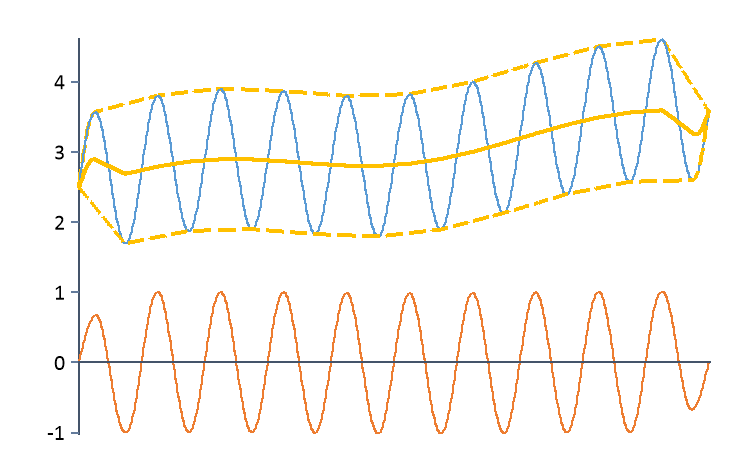
Adaptiv |
Subtrahiert den Mittelwert aus oberer und unterer Hüllkurve.
|
Gleitender Mittelwert |
Subtrahiert den gleitenden Mittelwert. Die zur Bildung des gleitenden Mittelwerts benötigte Intervallbreite kann eingegeben werden. Die Einstellung kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist. Der gleitende Mittelwertfilter ist ein Hochpassfilter.
|
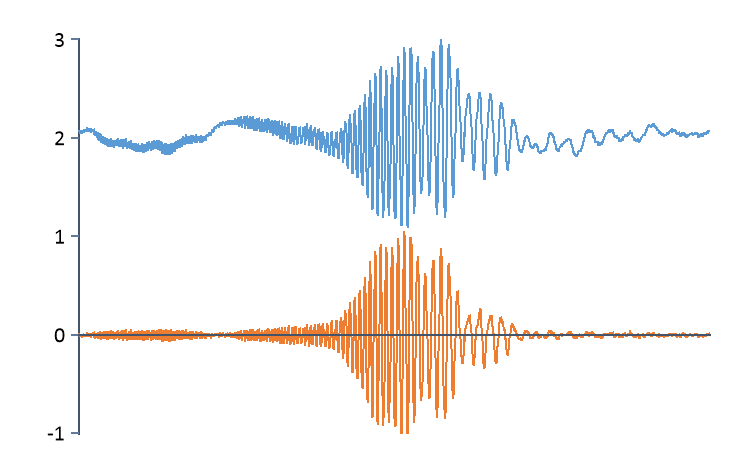
DC-Offset Filter |
Hochpassfilter zum Entfernen des DC-Offsets (IIR-Butterworth-Hochpass). Die Grenzfrequenz sowie die Ordnung (d.h. Steilheit) des Hochpassfilters kann eingestellt werden. Das Filter kann verwendet werden, wenn der vorliegende Trend weder konstant noch linear ist, sondern zeitabhängig ist.
|
Bei der Ermittlung des konstanten bzw. linearen Trends wird zunächst der Mittelwert des Signals berechnet und dann der erste und letzte Pegeldurchgang durch diesen Wert gesucht. Wenn zwei Pegeldurchgänge gefunden wurden, dann wird der Mittelwert bzw. die Bestgerade nur für den Bereich zwischen diesen beiden Pegeldurchgängen berechnet. Dies verhindert Fehler, die durch den Phasenanschnitt periodischer Signale an den Enden des Datensatzes auftreten. Wenn keine Pegeldurchgänge gefunden wurden, dann werden alle Werte in die Berechnung einbezogen. Passende Einstellungen zum Entfernen eines zeitabhängigen Trends ist gewöhnlich die Subtraktion des gleitenden Mittelwerts sowie der DC-Offset Filter.
Verwendete FPScript-Funktionen
* Dieses Analyseobjekt ist in FlexPro View nicht verfügbar.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen