SavitzkyGolayFilter (FPScript)
Filtert einen Datensatz mit einem Savitzky-Golay Glättungsfilter (auch bekannt als Least-Squares Glättung).
Syntax
SavitzkyGolayFilter(DataSet, SmoothingWidth, [ PolynomialOrder = 2 ] [ , Extrapolate = TRUE ])
Die Syntax der SavitzkyGolayFilter-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
|---|---|
DataSet |
Der zu filternde (glättende) Datensatz. Es sind alle Datenstrukturen erlaubt außer Einzelwert und Liste. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
SmoothingWidth |
Gibt an, wie viel benachbarte Werte inklusive des zu glättenden Wertes in die Glättung einbezogen werden sollen. Die Glättungsbreite sollte eine ungerade Zahl sein. Ansonsten ist das Intervall unsymmetrisch und es wird rechts vom Zentrum ein Wert mehr als links davon in die Berechnung einbezogen. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
PolynomialOrder |
Gibt die Ordnung des Polynoms an, das lokal an den Datensatz gefittet und somit zur Bestimmung der Filterkoeffizienten verwendet wird. Die Polynomordnung sollte kleiner als die Glättungsbreite gewählt werden (damit genügend Datenpunkte zur lokalen Polynomanpassung zur Verfügung stehen). Ansonsten wird die Polynomordnung für die Berechnung auf SmoothingWidth - 1 reduziert. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 0 und kleiner gleich 15 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 2 gesetzt. |
Extrapolate |
Der Wert TRUE gibt an, dass die Randpunkte zur Filterung symmetrisch verlängert werden. Die Filterkoeffizienten müssen in diesem Fall nur einmal berechnet werden. Die Extrapolation kann zwar zu einem irregulären Verhalten der Glättung an den Rändern führen, der Algorithmus bleibt aber schnell. Bei Wahl von FALSE wird die gleiche polynomiale Ordnung verwendet, um die Randpunkte zu glätten. Dabei bleiben an den Randpunkten die Glättungsbreite und die Ordnung des zu fittenden Polynoms gleich, während der Filtermittelpunkt in Richtung der Ränder verschoben wird. Die Filterkoeffizienten müssen also in diesem Falle für alle Randpunkte einzeln berechnet werden. Dies liefert in der Regel eine höhere Genauigkeit zur Glättung der Ränder, der Algorithmus ist aber erheblich langsamer. Erlaubte Datenstrukturen sind Einzelwert. Unterstützte Datentypen sind Wahrheitswert. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert TRUE gesetzt. |
Anmerkungen
Das Ergebnis hat die gleiche Struktur und Einheit wie das Argument DataSet.
Jeder Wert in DataSet wird mit (SmoothingWidth-1)/2 Nachbarwerten links und (SmoothingWidth-1)/2 Nachbarwerten rechts geglättet (wenn SmoothingWidth ungerade). Die Glättung entspricht dann einer Faltung des Signals mit Filterkoeffizienten der Länge SmoothingWidth. Bei diesem Verfahren werden die Filterkoeffizienten so bestimmt, dass das Ergebnis einer lokalen polynomialen Regression (d.h. lokalen polynomialen Kurvenanpassung) entspricht. Die Filterkoeffizienten sind dabei nicht von den y-Werten abhängig. Der Algorithmus ist beschrieben in SavitzkyGolay Algorithmus.
Die Filterung ist nicht auf die Unterdrückung höherer Frequenzen, sondern auf die Unterdrückung statistischer Momente höherer Ordnung optimiert. Das Filter eignet sich daher insbesondere zur Glättung von Signalen, die ohne Rauschen einen hohen Frequenzbereich aufweisen würden. Eingesetzt wird das Verfahren auch, wenn ein Peak durch nur wenige Punkte abgetastet wurde. Es lässt sich die Lage und die Höhe des Peaks schätzen, auch wenn das Maximum zwischen zwei Abtastpunkte fällt. Eine typische Anwendung ist zum Beispiel die Auswertung von Infrarot-Spektren. Das Savitzky-Golay-Glättungsverfahren wird auch "Digital Smoothing Polynomial Filter (DISPO)" oder "Least-Squares Smoothing" genannt.
Vor der Filterung werden die Werte in reelle bzw. komplexe 64-Bit Fließkommazahlen gewandelt. Das Ergebnis hat immer den Datentyp reelle oder komplexe 64-Bit Fließkommazahl.
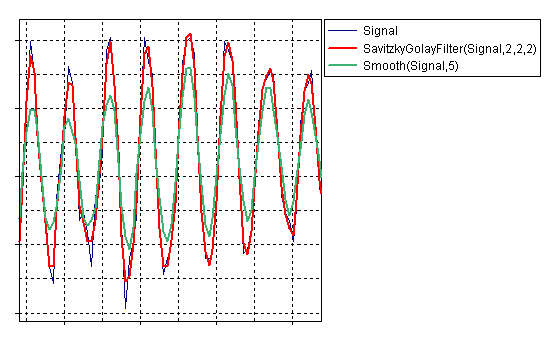
Die Grafik hebt den Unterschied der beiden Glättungsfunktionen Smooth (gleitender Mittelwert) und SavitzkyGolayFilter (mit polynomialer Ordnung 4) hervor. Beide Funktionen haben die gleiche Glättungsbreite. Während bei der Savitzky-Golay-Glättung der breiteste Peak gegenüber dem gleitenden Mittelwert weniger geglättet wird, behalten schmalere Peaks ihre Höhen und Breiten bei.
Verfügbarkeit
Option Digitale Filter
Beispiele
SavitzkyGolayFilter(Signal, 7, 2)
Glättet ein Signal mit dem Savitzky-Golay-Filter. Dazu wird ein Polynom zweiten Grades verwendet und es werden jeweils drei benachbarte Werte links und rechts des jeweils zu glättenden Wertes in das Ergebnis einbezogen (d.h. insgesamt 7 Werte).
SavitzkyGolayFilter(DataSet, N, 0)
Glättet einen Datensatz mit dem Savitzky-Golay-Filter durch lokale Kurvenanpassung mit einem Polynom der Ordnung 0. Dies entspricht einem gleitenden Mittelwert. Mit Ausnahme der Randstellen ist der Code daher äquivalent zu: Mean(DataSet, MEAN_ARITHMETIC + CALC_MOVING, N).
Dim N = 10
Dim polyOrder = 4
Dim width = 2*N + 1
Dim dirac = (0 # width) : 1 : (0 # width)
Dim coeff = SavitzkyGolayFilter(dirac, width, polyOrder)[N + 1, N + width]
AmplitudeResponse(coeff)
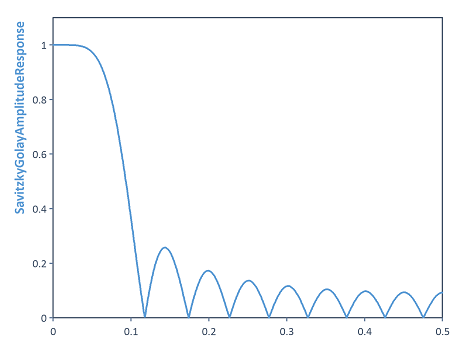
Berechnet den Amplitudengang des Savitzky-Golay-Filters (für polynomiale Ordnung 4 und Glättungsbreite 21). Hierzu wird die SavitzkyGolayFilter-Funktion auf einen Dirac-Stoß angewendet. Dies liefert die Übertragungsfunktion des Systems in Form der Filter-Koeffizienten. Mit Hilfe der Filter-Koeffizienten kann durch die AmplitudeResponse-Funktion der Amplitudengang des Filters berechnet werden.
Siehe auch
SavitzkyGolayDerivative-Funktion
Literatur
[1] Savitzky, A.; Golay, M.J.E.: Smoothing and Differentiation of Data by Simplified Least Squares Procedures. In: Analytical Chemistry, Vol. 36, No. 8, Pages 1627-39. http://pubs.acs.org/doi/abs/10.1021/ac60214a047,1964.
[2] A. Gorry: General least-squares smoothing and differentiation by the convolution (Savitzky–Golay) method. In: Analytical Chemistry, Vol. 62, No. 2, Pages 570-3. http://pubs.acs.org/doi/abs/10.1021/ac00205a007,1990.