Häufig werden zum Glätten von Daten Tiefpassfilter eingesetzt, die die hohen Frequenzen herausfiltern. Hochfrequente Schwankungen - insbesondere Messfehler - werden dadurch verringert.

Im Gegensatz zu den meisten Tiefpassfiltern, die im Fourier-Raum ansetzen, setzt der Savitzky-Golay-Filter im Zeitraum an. Man kann sich das Filter als ein Fenster vorstellen, das über die Daten gleitet und jedem Datenpunkt einen Mittelwert über das zugehörige Fenster zuordnet (moving window averaging):

gi ist der gefilterte Wert an der Stelle i.

fj ist der ungefilterte Wert an der Stelle j.

nL gibt die Datenpunkte links des zu glättenden Punkts an.

nR gibt die Datenpunkte rechts des zu glättenden Punkts an.

cn ist die Gewichtungsfunktion.

Die SavitzkyGolay-Filtermethode führt eine lokale polynomiale Regression durch, um die geglätteten Werte für jeden Datenpunkt zu bestimmen. Diese Methode ist der des gleitenden Durchschnitts überlegen, da sie Datenmerkmale wie Impulshöhe und Impulsbreite aufrechterhält, die normalerweise durch den gleitenden Durchschnitt ausgewaschen werden. Eingesetzt wird das Verfahren besonders, wenn ein Peak durch nur wenige Punkte abgetastet wurde. Es lässt sich die Lage und die Höhe des Peaks schätzen, auch wenn das Maximum zwischen zwei Abtastpunkte fällt.

Die Koeffizienten cn werden also so gewählt, dass höhere Momente erhalten bleiben. Im Gegensatz zum gleitenden Mittelwert werden die Koeffizienten nicht durch eine Konstante (geschätzt durch den Mittelwert) berechnet, sondern durch ein Polynom höherer Ordnung angegeben. Für die Berechnung wird eine Least-Squares-Schätzung verwendet. Glücklicherweise ist es nicht erforderlich, für jeden Punkt die Koeffizienten neu zu berechnen. Die Berechnung ist sogar unabhängig von den reellen Daten und hängt nur vom Grad des Polynoms ab. Die Anpassung wird durch eine Least-Squares-Schätzung (LS-Schätzung) zwischen der Matrix A und dem Vektor f durchgeführt:

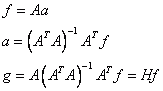
H wird auch die "hat"-Matrix genannt und ist für jedes f für ein gegebenes Polynom dasselbe. Sie kann also einmal berechnet und für eine spätere Anwendung gespeichert werden. Zur Berechnung der Koeffizienten muss nur eine einzelne Zeile der inversen Matrix berechnet werden. Diese kann man z.B. aus der LR-Zerlegung mit nur einer einzigen Rückwärtssubstitution erhalten.

Hinweis   Das SavitzkyGolay-Glättungsverfahren wird auch DISPO (Digital Smoothing Polynomial Filter) genannt.

Literatur

•Savitzky A., and Golay, M.J.E. (1964). Analytical Chemistry, vol. 36, p. 1627–1639.

•W. H. Press, et. al. (1992). Numerical Recipes in C, Second Edition. Cambridge University Press, p. 650-655.