MeshGrid (FPScript)
Erzeugt ein zweidimensionales Gitter. Hilfreich zur dreidimensionalen Visualisierung von Funktionen mit zwei Variablen oder von Funktionen mit komplexwertigen Argumenten.
Syntax
MeshGrid(X, Z)
Die Syntax der MeshGrid-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
|---|---|
X |
Definiert die Horizontale (X-Richtung) des zweidimensionalen Gitters. Erlaubte Datenstrukturen sind Datenreihe. Es sind alle numerischen Datentypen erlaubt. |
Z |
Definiert die Vertikale (Z-Richtung) des zweidimensionalen Gitters. Erlaubte Datenstrukturen sind Datenreihe. Es sind alle numerischen Datentypen erlaubt. |
Anmerkungen
Das Ergebnis hat immer die Datenstruktur Liste.
Die Funktion erzeugt aus zwei Datenreihen X der Länge N und Z der Länge M eine Liste mit zwei gleichnamigen Einträgen X und Z. Die Ergebniseinträge der Liste sind nun allerdings Matrizen bestehend aus N Zeilen und M Spalten, die durch Replikation der Funktionsargumente X bzw. Z gebildet werden. Die Einheiten der Ergebnismatrizen stimmen mit den Einheiten der einzelnen Argumente überein.
Das Ergebnis kann als zweidimensionales Rechteckgitter mit N x M Gitterpunkten wie folgt interpretiert werden: Gegeben seien beispielsweise die Datenreihe X als {1, 2, 3, 4} in horizontaler Richtung und die Datenreihe Z als {7, 8, 9} in vertikaler Richtung. Das Gitter, aufgespannt von X und Z, besteht nun aus den Koordinaten (1, 7), (2, 7), (3, 7), (4, 7), ..., (1, 9), (2, 9), (3, 9), (4, 9):
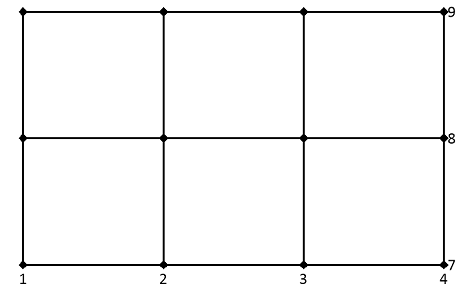
Die Koordinaten der einzelnen Gitterpunkte erhält man also elementweise aus den beiden gleichnamigen Matrizen:
Die Funktion MeshGrid angewendet auf die beiden Datenreihen liefert nun die Liste bestehend aus den gleichnamigen dargestellten Matrizen X (erstes Listenelement) und Z (zweites Listenelement).
Die Funktion wird gewöhnlich verwendet zur dreidimensionalen Darstellung von Funktionen y = f(x, z) zweier Veränderlicher über einem zweidimensionalen Rechteckgitter. Insbesondere können damit Funktionen y = f(z) = f(z1, z2) mit komplexwertigen Argumenten z = z1 + i * z2 über der komplexen Ebene berechnet und dargestellt werden.
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
Dim x = {1, 2, 3, 4}
Dim z = {7, 8, 9}
Dim grid = MeshGrid(x, z)
Dim y = grid.["X"]^2 - grid.["Z"] // = grid.[0]^2 - grid.[1]
Signal(y, x, z)
Beispiel 1: Vorgehen zur Berechnung von Funktionen mit zwei Veränderlichen
Berechnet die Funktion y = x^2 - z über dem Gitter aufgespannt durch die Datenreihen {1, 2, 3, 4} (in X-Richtung) und {7, 8, 9} (in Z-Richtung):

Dim x = Series(-4, 4, 0.01)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = ArcTan2(grid.["Z"], grid.["X"])
Signal(y, x, z)
Beispiel 2: Visualisierung der ArcTan2-Funktion mit 2 Variablen
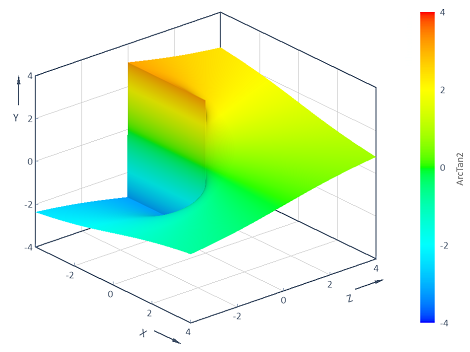
Berechnet die ArcTan2-Funktion y = f(x, z) = ArcTan2(z, x) über dem zweidimensionalen (x, z)-Bereich [-4, 4] x [-4, 4]. Die Visualisierung in einem 3D-Konturdiagramm liefert:
Dim x = Series(-16, 16, 0.04)
Dim z = x
Dim grid = MeshGrid(x, z)
Dim y = Sinc(Sqrt(grid.["X"]^2 + grid.["Z"]^2))
Signal(y, x, z)
Beispiel 3: Visualisierung der Sinc-Funktion in 2D
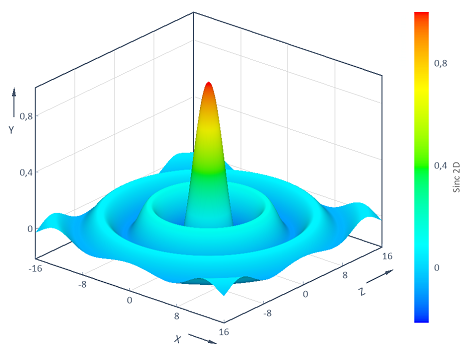
Berechnet die zweidimensionale Sinc-Funktion y = f(x, z) = Sinc(Sqrt(x^2 + z^2)) über dem zweidimensionalen (x, z)-Bereich [-16, 16] x [-16, 16]. Die Visualisierung in einem 3D-Konturdiagramm liefert:
Dim z1 = Series(-6, 6, 0.02)
Dim z2 = z1
Dim grid = MeshGrid(z1, z2)
Dim y = Real(Log(grid.[0] + 1i * grid.[1]))
Signal(y, z1, z2)
Beispiel 4: Visualisierung von Funktionen mit komplexen Argumenten
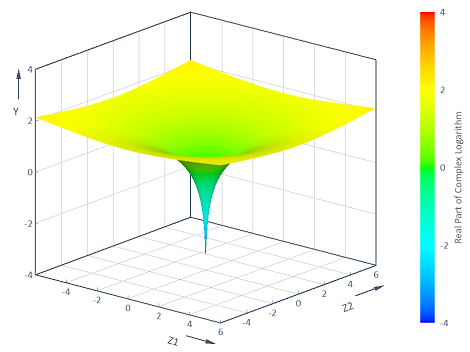
Berechnet den Realteil des komplexen Logarithmus y = f(z1, z2) = Real(Log(z1 + i* z2)) über der komplexen (z1, z2)-Ebene [-6, 6] x [-6, 6]. Die Visualisierung in einem 3D-Konturdiagramm liefert:
Arguments x, z
Dim xMatrix = x # NumberOfRows(z)
Dim zMatrix = TransposeMatrix(z # NumberOfRows(x))
List("X", xMatrix, "Z", zMatrix)
Beispiel 5: Äquivalenter FPScript Code
Diese FPScript-Funktion liefert das gleiche Resultat wie die MeshGrid-Funktion.
