LOESS/LOWESS Algorithmus
LOESS und LOWESS sind sehr verbreitete Glättungsverfahren mittels einer lokal gewichteten Regressionsfunktion (locally weighted regression).
Das Verfahren verwendet eine Gewichtungsfunktion, die dazu führt, dass der Einfluss benachbarten Wertes auf die Glättung an einer Position mit der Entfernung zu dieser Position abnimmt. Ausreißer werden geringer gewichtet als bei anderen Verfahren. Maßgeblich ist die Wahl der Glättungsbreite, welche die Anzahl der Werte, die in die Berechnung für einen Punkt eingehen, wiedergibt. Außerdem werden zwei Arten von Gewichten verwendet, die Nachbarschaftsgewichte und die Robustheitsgewichte.
1. Schritt:
Im ersten Verfahrensschritt erfolgt eine Festlegung des Bereichs der einzubeziehenden Punkte. Die Anzahl n dieser Punkte wird angegeben. Je größer dieser Wert ist, desto glatter wird letztendlich die angepasste Kurve. Der Bereich wird so festgelegt, dass genau n Werte inklusive des gewählten Punkts selbst im Bereich liegen und dass der gewählte Punkt im Zentrum des ausgewählten Bereichs liegt. Daher kann es vorkommen, dass die Anzahl an linken und rechten Nachbarn unterschiedlich groß sein kann. Der erste Wert hat zum Beispiel nur rechte Nachbarn.
2. Schritt:
Im zweiten Schritt werden die Gewichte für die lokal gewichtete Regressionsglättung festgelegt. Die Gewichtungsfunktion ist definiert durch:
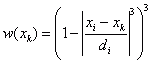
für k = 1,…,N
di ist der Abstand von xi zum N-ten Nachbarpunkt. Die Gewichtungsfunktion ist symmetrisch. Der größte Wert wird an der Stelle xi erreicht. An den Bereichsgrenzen ist der Wert 0.
3. Schritt:
Nun erfolgt ein Regressionsglättung. Für das LOWESS-Verfahren wird eine lineare Regressionsfunktion nach der Methode der kleinsten Quadrate geschätzt. Das LOESS-Verfahren verwendet dagegen eine quadratische Funktion
Die Parameter sind so zu berechnen, dass folgende Funktion minimiert wird:
LOWESS:
![]()
LOESS:
![]()
4. Schritt:
Bei der Schätzung der linearen Regressionsfunktion in den einzelnen Bereichen werden nur relativ wenige Beobachtungswerte einbezogen. Dadurch ist es immer möglich, dass die geschätzte Regressionsfunktion mehr oder weniger stark durch potentielle Ausreißer beeinflusst wird. Deshalb werden in einem vierten Schritt die so genannten Robustheitsgewichte ermittelt. Für die Ermittlung der Gewichte werden die Residuen der bisher geschätzten Werte und daraus der Median berechnet.
Die Robustheitsgewichte werden mit folgender Formel errechnet:
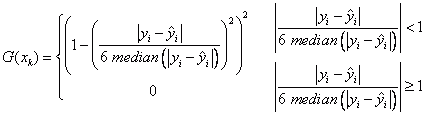
Das Robustheitsgewicht ist 0, wenn ein Residuum größer gleich 6m (m = Median Residuen) ist. Dadurch werden Ausreißer eliminiert.
Die Robustheitsgewichte, multipliziert mit den Nachbarschaftsgewichten, werden für eine erneute Schätzung einer linearen Regressionsfunktion innerhalb der einzelnen Bereiche verwendet:
LOWESS:
![]()
LOESS:
![]()
Dadurch ergibt sich eine Reihe neuer geglätteter Werte. Die Prozedur kann mehrfach wiederholt werden Je höher die Anzahl der Iterationen ist, desto genauer ist die Kurvenanpassung, wobei jedoch die weitere Erhöhung einer bereits hohen Iterationsanzahl kaum eine sichtbare Verbesserung bringt.
Literatur
•Cleveland, W.S. (1979). Robust Locally Weighted Regression and Smoothing Scatterplots. Journal of the American Statistical Association, Vol. 74, pp. 829-836.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen