Analyseobjekt IIR-Filter (Option Digitale Filter)
Mit diesem Analyseobjekt können Sie Signale filtern. Es werden Tiefpass, Hochpass, Bandpass und Bandsperre mit verschiedenen Charakteristika angeboten.
Das Objekt arbeitet mit Infinite-Impulse-Response (IIR) Filtern, welche über interne Rückkopplungen verfügen (Rekursive Filter).
Ergebnis
Als Ergebnis können die berechneten Filterkoeffizienten oder die Pol- und Nullstellen ausgegeben werden. Das Ergebnis ist jeweils eine Liste mit den Zähler- und Nennerkoeffizienten bzw. den Polen und Nullstellen. In diesem Fall muss kein Eingangsdatensatz angegeben werden. Alternativ kann das Ergebnis ein Signal sein, das mit dem zuvor berechneten IIR-Filter gefiltert wird. Hierzu muss in der Registerkarte Daten ein zu filternder Datensatz ausgewählt werden. Im Gegensatz zum Ergebnis Gefiltertes Signal werden die Daten beim Ergebnis Gefiltertes Signal mit Phasenkorrektur zweimal gefiltert, einmal vorwärts und einmal rückwärts. So werden Phasenverschiebungen vermieden.
Filtercharakteristik
Es stehen Filter mit folgenden Eigenschaften zur Verfügung:
•Bessel-Filter: Filter mit gutem Rechteck-Übertragungsverhalten und flachem Durchlassbereich, jedoch mit relativ geringer Steilheit.
•Butterworth-Filter: Filter mit flachem Durchlassbereich und hoher Flankensteilheit, jedoch instabil bei steilflankigen Eingangssignalen.
•Tschebyscheff-Filter: Noch steiler als das Butterworth-Filter, jedoch mit Welligkeit im Durchlassbereich. Diese Welligkeit kann auf Kosten der Steilheit vermindert werden.
•Invers-Tschebyscheff-Filter (Tschebyscheff II-Filter): Zeigt eine gleichmäßige Welligkeit (Ripple) im Sperrbereich. Die Dämpfung steigt auch bei großem Abstand von der Grenzfrequenz nicht über einen bestimmten Wert.
•Elliptischer Filter (Cauer-Filter): Das Filter besitzt eine noch größere Filtersteilheit, bei gleichmäßiger Welligkeit im Durchlass- und Sperrbereich und nichtlinearem Phasengang. Diese Filtercharakteristik wird bevorzugt als Anti-Aliasing-Filter in CW-Anwendungen (CW: Continuous Wave) eingesetzt. Das Filter wird durch eine elliptische Differentialgleichung beschrieben.
Filtertyp
Die Filter können alle als Tiefpass, Hochpass, Bandpass und Bandsperre verwendet werden.
Ordnung
Die Filterordnung bestimmt die Steilheit des Filters. Je höher die Ordnung, desto höher ist auch die Steilheit des Filters. Hohe Filterordnungen können jedoch bei IIR-Filtern zur Instabilität führen. Es ist möglich, eine feste Ordnung anzugeben oder die Ordnung zu schätzen. In diesem Fall müssen Sie statt der Eckfrequenzen die Übergangsbereiche angeben.
Eckfrequenz / Übergang
Bei einer festen Filterordnung müssen Sie für Tiefpass- bzw. Hochpassfilter eine Eckfrequenz angeben. Bei einem Bandpass bzw. einer Bandsperre sind zwei Eckfrequenzen erforderlich. Wird die Filterordnung geschätzt, so geben Sie die untere und obere Grenze für einen (Tiefpass, Hochpass) bzw. zwei (Bandpass und Bandsperre) Übergangsbereiche an.
Wenn Sie die Option Normierte Frequenzen verwenden anklicken, werden alle Frequenzangaben auf die Abtastfrequenz normiert. Ansonsten geben Sie die Frequenzen in der Einheit an, die dem Kehrwert der Zeiteinheit des zu filternden Signals entspricht. Wegen der Nyquist-Grenze sind nur Werte bis maximal 0,5 bzw. bis zur halben Abtastfrequenz zulässig.
Spezifikation
Für das Tschebyscheff-Filter kann die Welligkeit Ap frei gewählt werden, für das inverse Tschebyscheff-Filter kann die Dämpfung Aa angegeben werden und für das Elliptische Filter wird sowohl die Welligkeit als auch die Dämpfung angegeben. Alternativ zur Welligkeit und Dämpfung kann der Fehler im Durchlassbereich δp und der Fehler im Sperrbereich δa angegeben werden, wenn als Modus Fehler(Delta) statt Modus Welligkeit/Dämpfung gewählt wird.
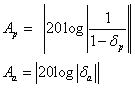
Amplitudengang, Phasengang, Gruppenlaufzeit (Nur Analyseassistent)
Wählen Sie diese Optionen, um zusätzliche Diagramme anzuzeigen. Der Amplitudengang zeigt, wie stark einzelne Frequenzen gedämpft werden. Der Phasengang und die Gruppenlaufzeit zeigen an, wie stark diese verzögert werden. Hat eine Frequenz von 100Hz, z. B. eine Phase von -180°, dann bedeutet dies, dass diese um eine halbe Periodendauer, d. h. um 5ms verzögert wird. Die Verzögerung ist für alle Frequenzen gleich, wenn der Phasengang eine schräg abfallende Gerade ist. Die Gruppenlaufzeit ist dann eine horizontale Linie.
Beispiel
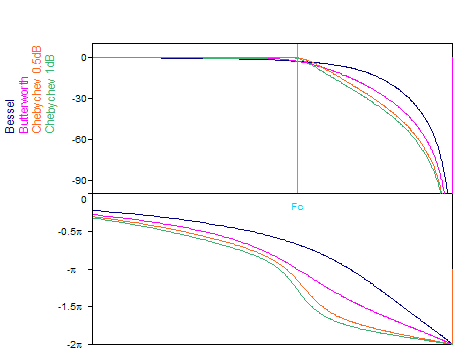
Folgende Grafik zeigt das Bode-Diagramm mit dem Betrags- und Phasenverlauf einiger Filter vierter Ordnung:
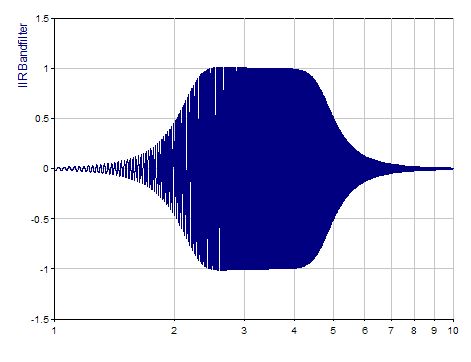
Folgende Grafik zeigt ein Wobbelsignal, welches mit einem Butterworth-Bandpass vierter Ordnung gefiltert wurde. In der logarithmischen X-Darstellung erscheinen beide Flanken gleich steil:
