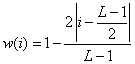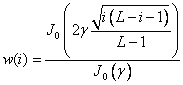Die Entwurfstechniken für FIR-Filter basieren auf der direkten Approximation des gewünschten Frequenzgangs des zeitdiskreten Systems. Die Filterkoeffizienten entsprechen hierbei der Impulsantwort des zu realisierenden Filters. Um verschiedene Signale verarbeiten zu können, ist es notwendig, dass diese Signale endlich sind. Dies ist jedoch nicht immer der Fall. Um solche endliche Signal-Folgen aus unendlichen Folgen zu generieren verwendet man häufig die Fenstertechnik. Dieses "Abschneiden" einer unendlichen Folge zur endlichen Folge hat jedoch auch Auswirkungen im Frequenzbereich. Vom Prinzip her wäre diese Methode exakt, da aber nur endlich viele Werte verwendet werden können, weist dieses Prinzip mehr oder weniger große Abweichungen auf, die sich vor allem in der erreichbaren Sperrdämpfung und Flankensteilheit störend äußern.

Die Approximation eines idealen Filters durch Abschneiden der idealen Impulsantwort ist identisch mit dem Konvergenzproblem der Fourier-Reihen. Durch das Verhalten von Fourierreihen bei Unstetigkeitsstellen entsteht immer eine Welligkeit im Durchlass und Sperrbereich. Sie ist grundsätzlich zu beobachten, wenn mit Fourierreihen eine unstetige Funktion modelliert wird. Die Welligkeit verschwindet auch nicht, wenn die Zahl der Koeffizienten erhöht wird, sondern konzentriert sich nur stärker im Bereich der Grenzfrequenz. Dieser Effekt wird Gibbs-Phänomen genannt. Abhilfe kann durch geeignete Gewichtung der Filterkoeffizienten erfolgen. Hierbei werden die Randkoeffizienten geeignet reduziert. Allerdings steigt auch die benötigte Filterordnung bei gleicher Flankensteilheit.

Fenster-Funktionen

Die nicht idealen Effekte, die aufgrund der endlichen Anzahl Filterkoeffizienten zu beobachten sind, kann durch Benutzung eines Gewichtsfensters gemildert werden. Das Prinzip dabei ist, dass die mittleren Filterkoeffizienten stärker gewichtet werden als die Koeffizienten am Anfang und Ende.

Es gibt zahlreiche Fensterfunktionen, die die maximal erreichbare Sperrdämpfung definieren:

Mit dieser Maßnahme wird vor allem das Sperrverhalten verbessert. Im Gegenzug verschlechtert sich aber die Flankensteilheit und das Signal erfährt eine zusätzliche Dämpfung. Näherungsweise kann man sagen, dass je stärker die erreichte Sperrdämpfung ansteigt, desto mehr verschlechtert sich die Flankensteilheit bei gleicher Filterlänge L. Natürlich kann wiederum die Filterlänge erhöht werden um die Flankensteilheit zu verbessern.

Grundsätzlich sind Kaiser-Fenster die beste Wahl bezüglich erreichter Flankensteilheit/Filterlänge und erreichter Sperrdämpfung. Zusätzlich existiert für Kaiser-Filter eine heuristische Formel, die aus den Sperrforderungen die notwendige Filterordnung abschätzt.

Eine Beschreibung der Tschebyscheff-Fensterfunktion (Dolph-Chebyshev Window) befindet sich in Antoniou, p.440.

Filterentwurfsmethode mit Kaiser-Fenster

Eine besondere Rolle nimmt das Kaiser-Fenster ein. Der Kompromiss zwischen der Breite des Hauptmaximums (mainlobe) und der Dämpfung der Nebenmaxima (sidelobe) kann durch die Suche nach einem Fenster quantifiziert werden, das im Frequenzbereich um ω = 0 maximal konzentriert ist. Kaiser (1966, 1974) fand heraus, dass ein nahezu optimales Fenster mithilfe einer modifizierten Bessel-Funktion erster Art und nullter Ordnung gefunden werden kann.

Dieses Fenster kann so angepasst werden, dass zwischen Amplitude des Nebenmaximums und Breite des Hauptmaximums ein Kompromiss gefunden werden kann. Wie bei der Tschebyscheff-Funktion kann auch beim Kaiser-Fenster die Filterlänge L über die Angaben Dämpfung und Übergang berechnet werden. Die Filterlänge ist die kleinste ungerade Zahl, die folgende empirisch ermittelte Ungleichung erfüllt.

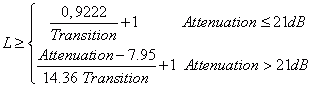
Zum Beispiel ist für einen Filterentwurf mit einer Dämpfung von 30dB im Sperrbereich und einem Übergangbereich von 0,1 (normierte Frequenz) mindestens eine Filterlänge von 17 erforderlich.

Algorithmus

Der in FlexPro verwendete Algorithmus basiert auf dem Programm FIR1 von L.R. Rabiner, C.A. McGonegal und D. Paul.

Literatur

•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.

•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.

•L. R. Rabiner, C. A. McGonegal and D. Paul (1979). FIR Windowed Filter Design Program - WINDOW. Section 5.2 in Programs for Digital Signal Processing, IEEE Press, pp. 5.2-1 to 5.2-19.