FIR-Equiripple Algorithmus
Der Entwurf von FIR-Filtern mit der Fenstermethode hat den Nachteil, dass der Approximationsfehler in verschiedenen Frequenzbereichen nicht beeinflusst werden kann. Daher ist es oft besser, für den Filterentwurf die Minimax-Strategie (Minimierung des maximalen Fehlers) oder ein Fehlerkriterium mit Wichtung der Frequenz einzuführen. Dies führt zum "besten" Filter, der für eine vorgegebene Spezifikation erzielt werden kann.
Die FIR-Equiripple Methode, die auch unter den Namen Remez-Exchange Methode, Parks-McClellan bekannt ist, liefert immer die FIR-Filter mit minimaler Filterlänge. Das Verfahren von Parks-McClellan liefert mit dem Remez-Exchange Algorithmus in einem Iterationsverfahren die Lösung eines Filters. Da mit diesem Näherungsverfahren Filter mit konstanter Welligkeit sowohl im Durchlass- als auch im Sperrbereich erzeugt werden können, nennt man die Filter auch Equiripple-Filter.
Der Remez-Exchange Algorithmus ist ein auf Tschebyscheff-Polynomen beruhender Optimierungsalgorithmus. Für den gewünschten Filter wird eine Fehlerfunktion aus einer Linearkombination von Kosinus-Funktionen gebildet und durch ein effizientes Optimierungsverfahren minimiert.
Minimax- oder Tschebyscheff-Kriterium
Bei diesem Entwurfsverfahren wird das so genannte Tschebyscheff- oder Minimax-Kriterium verwendet. Dabei wird in festgelegten Frequenzintervallen ein Frequenzgang A(ejω) gesucht, der den maximalen gewichteten Approximationsfehler der Fehlerfunktion minimiert. Dazu wird folgende Fehlerfunktion aufgestellt:
![]()
E(ω) … Fehlerfunktion
W(ω) … Wichtungsfunktion
H(ejω) … gewünschter Frequenzgang
A(ejω) … Approximationsfunktion
Die Fehlerfunktion, die Wichtungsfunktion und der gewünschte Frequenzgang sind nur für abgeschlossene Teilintervalle des normierten Frequenzbereichs 0 <= ω <= 0,5 definiert. Ein Tiefpassfilter besitzt z.B. die Intervalle 0 <= ω <= ωp und ωs <= ω <= 0,5. Im Übergangsbereich ist die Approximationsfunktion nicht beschränkt und kann daher jede Form annehmen, da hier keine Fehlerschranken definiert sind.
Es lassen sich Filter für frei definierte Frequenzgänge entwerfen. Dazu kann man den gewünschten Frequenzgang als Signal übergeben, dessen Y-Komponente die Amplituden als kontinuierliche Kurve und dessen X-Komponente die dazugehörigen normierten Frequenzen (Bereich 0 - 0,5) enthält.
Prinzip des Remez-Exchange Algorithmus
Das Verfahren basiert auf der Umformulierung der Aufgabe des Filterentwurfs in eine Aufgabe für eine Polynomapproximation. Mit einem Iterationsverfahren wird eine eindeutige polynomiale Funktion pn(x), die innerhalb eines Fehlerbandes ±h die Vorgaben pn(xi)=yi±h erfüllt, approximiert. Das Polynom oszilliert innerhalb des Fehlerbandes in den lokalen Extremwerten um ±h. Der Polynomgrad n und das Fehlerband ±h kann frei gewählt werden. Dabei wird das so genannte Alternantentheorem angewandt, das u. a. in Oppenheim und Schafer ausführlich beschrieben wird.
1. Die Bestimmung des Ausgleichspolynoms pn(x) vom Grad n für eine Menge von n+2 Datenpunkten (xi, yi) erfolgt durch Lösung des linearen Gleichungssystems für die Polynomkoeffizienten a0..an und den Fehler h. Vorgegeben sind die zu erreichenden Funktionswerte yi (i=1..n+2). Man erhält daher ein Gleichungssystem mit n+2 Gleichungen:
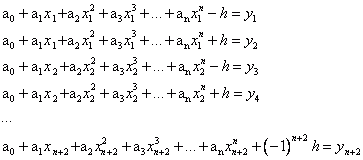
2. Bestimmung der n+2 Extrema der Abweichungen von der Vorgabe.
3. Bestimmung des neuen Ausgleichspolynom vom Grad n unter Verwendung neuer Werte xi, die an den Extrema liegen, wie in 1.
4. Algorithmus wiederholen bis der Fehler ±h den Vorgaben genügt.
Das Verfahren ist sehr flexibel und kann verwendet werden, um optimale Lösungen für die meisten nicht-rekursiven Filter (z.B. digitaler Differenzierer, Hilbert Transformierer, Tiefpass-, Hochpass-, Bandpass-, Multiband-Filter mit einer stückweise konstanten Amplitudenantwort) zu errechnen. Es ist sogar möglich, einen beliebigen Amplitudengang vorzugeben und daraus den optimalen Filter zu ermitteln.
Einer der populärsten Computeralgorithmen, der auf dem Remez-Exchange Algorithmus beruht, stammt von James H. McClellan, Thomas W. Parks und Lawrence R. Rabiner und ist auch als Parks-McClellan-Verfahren bekannt. Der in FlexPro verwendete Algorithmus beruht auf diesem Algorithmus. Es lassen sich sowohl Filter mit vorgegebener Filterlänge entwerfen als auch optimale Filter anhand einer vorgegebenen Spezifikation ermitteln.
Gewichtung der Fehler und Fehlergrenzen
Es gibt zwei Möglichkeiten, einen FIR-Filter zu berechnen. Entweder können Sie die Filterlänge angeben oder Sie können eine Spezifikation vorgeben und daraus die Länge des Filters errechnen.
Vorgegebene Filterlänge
Wird eine Filterlänge angegeben, so lässt sich nur das Verhältnis der Fehler der einzelnen Bänder angeben, da nicht sichergestellt ist, ob mit der angegebenen Filterlänge die gewünschte Spezifikation (absolute Fehlergrenzen) eingehalten werden kann.
Die vorgegebene Filterlänge entspricht der Länge der Impulsantwort. In diesem Fall wird die Gewichtung der Fehler der einzelnen Bänder angegeben. Die Gewichtungsfaktoren stehen in Relation zueinander. Bei einem Multibandfilter mit drei Bändern besagt zum Beispiel die Gewichtungsangabe {1, 10, 1}, dass das zweite Band eine 10mal niedrigere Welligkeit als die anderen beiden Bänder hat. Dieser Bereich ist somit glatter. Wenn die Gewichtung nicht angegeben wird, so haben alle Bänder das gleiche Gewichtungsverhältnis.
Vorgeschriebene Spezifikation
In diesem Fall wird die Filterlänge nicht angegeben. Stattdessen werden die gewünschten Fehlergrenzen angegeben. Anhand dieser Angaben wird die Filterlänge L mit folgender Formel empirisch geschätzt:

[Quelle: Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York, p. 701]
Diese Formel gilt nur für Tiefpass- bzw. Hochpassfilter. Für Multibandfilter wird für jeden Übergang von einem Band zum nächsten die Filterlänge geschätzt. Der größte Wert wird als Startwert übernommen. Anschließend wird die Filterlänge solange vergrößert bzw. verringert, bis der optimale Filter für die gewünschte Spezifikation ermittelt wurde.
Das Verfahren ist nur numerisch lösbar und daher für hohe Ordnungen relativ aufwendig. Allerdings liefert es im Gegensatz zur Fenster-Methode eine optimale Lösung. Es kann jedoch passieren, dass der Algorithmus aufgrund von Konvergenzproblemen keine Lösung findet.
Literatur
•Oppenheim, A. V. and Schafer, R. W. (1999). Discrete-Time Signal Processing, 2nd Edition. Prentice Hall, New Jersey.
•Antoniou, Andreas (2005). Digital Signal Processing. McGraw-Hill, New York.
•J. H. McClellan, T. W. Parks, L. R. Rabiner. A Computer Program for Designing Optimum FIR Linear Phase Digital Filters. IEEE Transactions on Audio and Electroacoustics, Vol. AU-21, No.6, December 1973
•L. R. Rabiner, J. H. McClellan and T. W. Parks. FIR Digital Filter Design Techniques Using Chebyshev Approximation. Proceedings IEEE, Vol. 63, No. 4, pp. 595 610, April 1975
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen