Distribution (FPScript)
Berechnet verschiedene Verteilungs- oder Dichtefunktionen.
Syntax
Distribution(X, Distribution, Parameter1 [ , Parameter2 ])
Die Syntax der Distribution-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
X |
Enthält die X-Werte, d. h. die Werte der Zufallsvariablen, für die die Verteilungsfunktion bzw. die Dichtefunktion berechnet werden soll. Bei Berechnung einer diskreten Verteilung müssen die X-Werte ganzzahlig und positiv sein. Erlaubte Datenstrukturen sind Einzelwert, Datenreihe und Datenmatrix. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||||||||||||||
Distribution |
Gibt an, welche Verteilung berechnet werden soll, und ob die Verteilungs- oder die Dichtefunktion berechnet werden soll. Das Argument Distribution kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||||||||||||||
Parameter1 |
Gibt den ersten Parameter der zu berechnenden Verteilung an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||||||||||||||
Parameter2 |
Gibt, falls benötigt, den zweiten Parameter der zu berechnenden Verteilung an. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Die Verteilungen werden anhand diverser Näherungsformeln berechnet. Bevor Sie die mit dieser Funktion berechneten Verteilungen für statistische Zwecke verwenden, sollten Sie daher prüfen, ob die Genauigkeit für Ihre Aufgabe ausreicht.
Verfügbarkeit
Option Erweiterte Statistik
Beispiele
Dim x = (100, -5, 0.101010101010101)
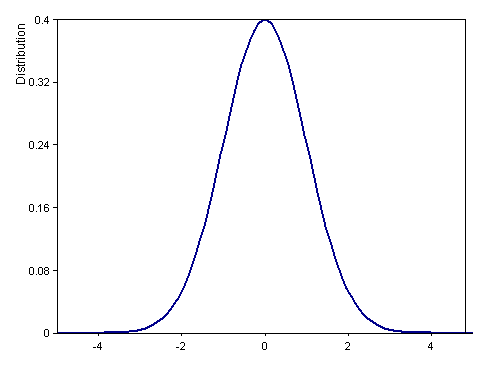
Signal(Distribution(x, DISTRIBUTION_NORMAL + DISTRIBUTION_DENSITY, 0, 1), x)
Berechnet die Dichtefunktion der Standardnormalverteilung (Erwartungswert 0, Varianz 1) im Intervall [-5, 5].
Siehe auch
Literatur
[1] "Hartung, Joachim": "Statistik, 9. Auflage". "Oldenbourg Verlag GmbH, München",1993.ISBN 3-486-22055-1.