DCRemovalFilter (FPScript)
Entfernt den DC-Offset (DC-Bias oder Gleichanteil) mit Hilfe eines digitalen (rekursiven) Hochpassfilter.
Syntax
DCRemovalFilter(DataSet, [ CutOffFrequency = 0.01 ], [ SamplingRate ], [ Order = 1 ] [ , PhaseCorrection = True ])
oder
DCRemovalFilter(Result, [ CutOffFrequency = 0.01 ], [ SamplingRate ] [ , Order = 1 ])
Die Syntax der DCRemovalFilter-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||
|---|---|---|---|---|---|---|---|---|---|
DataSet |
Der Datensatz, aus dem der DC Offset entfernt werden soll. Erlaubte Datenstrukturen sind Datenreihe, Datenmatrix, Signal und Signalreihe. Es sind alle numerischen Datentypen erlaubt. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||
CutOffFrequency |
Gibt die Grenzfrequenz des Hochpassfilters an. Die Frequenz muss zwischen 0 und 0,25 (ein Viertel der auf Eins normierten Abtastrate) oder zwischen 0 und 0,25 * SamplingRate liegen. Die Grenzfrequenz ist definiert als die Frequenz, bei der die Amplitude des Filters 70,7 Prozent der ursprünglichen Signalamplitude übersteigt. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Der Wert muss größer gleich 0 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 0,01 gesetzt. |
||||||||
SamplingRate |
Gibt die Abtastrate an. Das Argument ist optional. Wird dieses Argument nicht spezifiziert, so muss als Grenzfrequenz für CutOffFrequency eine normierte Frequenz von 0 bis 0,25 angegeben werden. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle reellen Datentypen erlaubt außer Kalenderzeit und Zeitspanne. Der Wert muss größer 0 sein. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||
Order |
Gibt die Ordnung des DC-Removal-Filters an. Eine Erhöhung der Ordnung bewirkt eine Vergrößerung der Steilheit des Hochpassfilters. Im Gegenzug verursachen höhere Ordnungen aber längere Berechnungs- und Filtereinschwingzeiten. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 und kleiner gleich 10 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert 1 gesetzt. |
||||||||
PhaseCorrection |
Der Wert TRUE gibt an, dass die Filterung inklusive zusätzlicher Phasenkorrektur erfolgt, d.h. das gefilterte Signal besitzt die gleiche Phase wie das Eingangssignal. Hierzu wird zweimal gefiltert, einmal vorwärts und einmal rückwärts. Erlaubte Datenstrukturen sind Einzelwert. Unterstützte Datentypen sind Wahrheitswert. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert True gesetzt. |
||||||||
Result |
Gibt an, ob als Ergebnis die Filterkoeffizienten oder die Pol- und Nullstellen des Filters zurückgegeben werden. Das Argument Result kann folgende Werte haben:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Filter entspricht einem Butterworth-Hochpassfilter mit der spezifizierten Ordnung Order und Grenzfrequenz CutOffFrequency. Der Butterworth-Hochpassfilter kann alternativ ebenso mittels der IIRFilter-Funktion entworfen werden.
Verwenden Sie die erste Syntax, um direkt den DC-Offset von Signalen zu entfernen. Die Struktur des Ergebnisses entspricht der des Arguments DataSet. Bei Datenmatrizen und Signalreihen erfolgt die Berechnung spaltenweise. Die X- bzw. Z-Komponenten werden, falls vorhanden, unverändert in das Ergebnis übernommen.
Verwenden Sie die zweite Syntax, um die Zähler- und Nennerkoeffizienten des Filters als Liste mit zwei Elementen b und a oder die Pol- und Nullstellen des Filters zurückgegeben. Die Zähler- und Nennerkoeffizienten können verwendet werden, um den Amplitudengang des Filters mittels AmplitudeResponse oder den Phasengang mittels PhaseResponse auszurechnen.
Das Filter besitzt den folgenden Amplitudengang (Order = 1) für verschiedene Grenzfrequenzen. Der DC-Anteil wird herausgefiltert, Frequenzen oberhalb der Grenzfrequenz werden annähernd ungeschwächt durchgelassen:
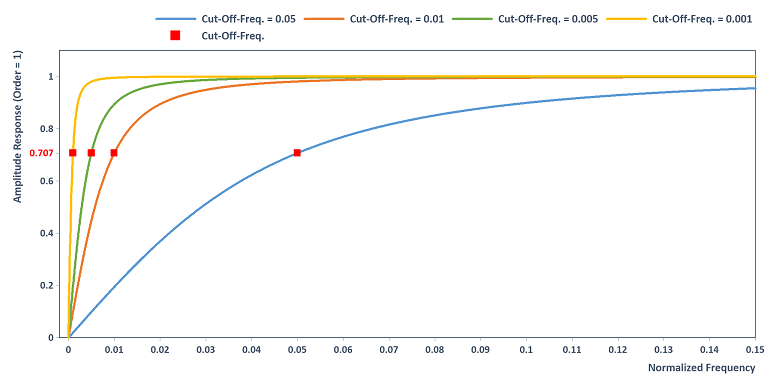
Eine Erhöhung der Ordnung bewirkt eine Vergrößerung der Steilheit des Hochpassfilter, beispielsweise bei Wahl von Order = 3:
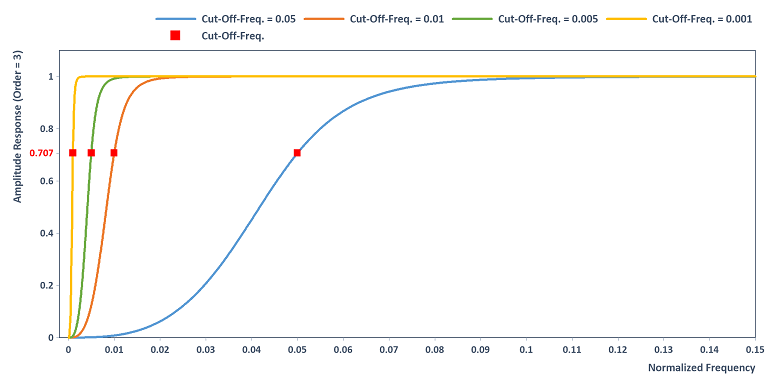
Hinweis Für die Vorgabeeinstellung Order = 1 reduziert sich das Filter auf einen gängigen rekursiven Filter erster Ordnung zum Entfernen des DC-Offsets, auch bekannt unter dem Namen Cascaded-Differentiation-Integration-Filter, siehe [1, Sektion 13.23] oder [2]. Interpretation dieser Namensgebung: Der Cascaded-Differentiation-Integration-Filter wird gebildet aus rückwärts gerichteter Differentiation, gefolgt von anschließender "Leaky"-Integration mit Rückkopplungskonstanten . Der digitale Differentiator entfernt den DC-Anteil, der anschließende Integrator liefert das Eingangssignal ohne DC-Offset zurück. Der Cascaded-Differentiation-Integration-Filter (CDI) besitzt dabei die folgende rekursive Definitionsvorschrift:
Der Parameter aus dem Intervall [0, 1] kann eindeutig durch die normierte Grenzfrequenz ω aus dem Intervall [0, 1/4] wie folgt berechnet werden:
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
DCRemovalFilter(DataSet)
Entfernt den DC-Bias eines Datensatzes. Die normierte Grenzfrequenz wird standardmäßig auf die normierte Frequenz von 0,01 gesetzt. Dies entspricht einer Grenzfrequenz von einem Hundertstel der Abtastfrequenz.
DCRemovalFilter(DataSet, 3 Hz, SamplingRate(Signal.X))
Entfernt den DC-Bias eines Datensatzes. Die Grenzfrequenz wird auf 3 Hz gesetzt. Dies entspricht einer normierten Grenzfrequenz von 3 Hz / Abtastfrequenz.
Integral(DCRemovalFilter(Signal))
Integriert ein Signal und entfernt vorher den Drift bzw. DC-Offset. Begründung: Wenn Sie Signale integrieren, die einen Drift oder DC-Offset besitzen, dann läuft die integrierte Kurve weg. Ursache hierfür ist nicht nur die Akkumulation des DC-Offsets während der Integration, sondern auch der zur Frequenz umgekehrt proportionale Amplitudengang des Integrators (siehe Integral-Funktion). Durch diesen wird Rauschen bei Frequenzen nahe dem DC-Anteil verstärkt und durch die Integration auf beliebig große Werte angehoben. Die integrierte Kurve läuft dann weg. Folgende Grafik verdeutlicht diesen Sachverhalt (exemplarisch wurde zur Integration eines der Beschleunigungssignale aus den FlexPro-Beispieldaten unter C:\Users\Public\Documents\Weisang\FlexPro verwendet):
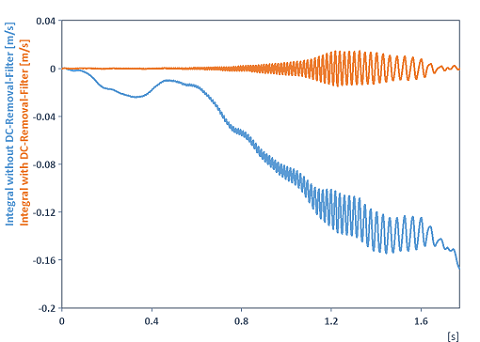
Dim coeff = DCRemovalFilter(FILTER_COEFFICIENTSCASCADED, 0.01, , 3)
AmplitudeResponse(coeff, 100000)
Berechnet den Amplitudengang (mit 100000 Datenpunkten) des DC-Removal-Filters für die normierte Grenzfrequenz 0,01 und Ordnung 3 mit Hilfe der AmplitudeResponse-Funktion.
Dim coeff = DCRemovalFilter(FILTER_COEFFICIENTSCASCADED, 0.01)
Filter(Signal, coeff, TRUE)
Es werden zuerst die Zähler- und Nennerkoeffizienten des Filters berechnet, anschließend die Daten mit der Filter-Funktion gefiltert. Der Code ist äquivalent zu: DCRemovalFilter(Signal).
Dim param = DCRemovalFilter(FILTER_POLESANDZEROS, 0.001, , 5)
Signal(Imag(param.Poles), Real(param.Poles))
Berechnet die Polstellen des Filters zur normierten Grenzfrequenz 0,001 und Ordnung 5 und gibt diese in der Datensatzstruktur Signal zurück. Es sei angemerkt, dass eine zu hohe Ordnung numerische Artefakte für zu klein gewählte Grenzfrequenzen verursachen kann. Die numerischen Artefakte sind mathematisch dadurch bedingt, wenn die Polstellen des Filters auf dem Einheitskreis liegen oder diesem sehr nahe kommen. Beispielsweise sind für Order = 1 die Polstellen weiter vom Einheitskreis entfernt als für Order = 5. Das numerisch stabilste Filter erhalten wir also für Order = 1.
Siehe auch
Literatur
[1] Richard G. Lyons: Understanding Digital Signal Processing (3rd Edition). Prentice Hall,2011.ISBN 0-13-702741-9.
[2] Richard G. Lyons, Randy Yates: DC Blocker Algorithms. In: IEEE Signal Processing Magazine, Vol. 25, Issue 2. 2008.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen