CoefficientOfVariation (FPScript)
Berechnet den absoluten oder relativen Variationskoeffizienten für einen Datensatz.
Syntax
CoefficientOfVariation(DataSet, [ Mode = CV_ABSOLUTE + PROCESS_ROWS ] [ , IntervalWidth ])
Die Syntax der CoefficientOfVariation-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
Der auszuwertende Datensatz. Es sind alle Datenstrukturen erlaubt. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||||||||||||
Mode |
Gibt an, wie Datenmatrizen und Signalreihen verarbeitet werden sollen und ob einzelne, gleitende oder Blockkoeffizienten ermittelt werden sollen. Das Argument Mode kann folgende Werte haben:
...plus einer Konstante, die die Verarbeitung von Datenmatrizen und Signalreihen bestimmt...
... plus einer optionalen Konstanten, die die Berechnungsweise bestimmt:
Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. Wenn das Argument nicht angegeben wird, wird es auf den Vorgabewert CV_ABSOLUTE + PROCESS_ROWS gesetzt. |
||||||||||||||||||||
IntervalWidth |
Dieses Argument wird für die Ermittlung von gleitenden und Blockkoeffizienten benötigt. Die Intervallbreite gibt dann die Anzahl der zu betrachtenden Werte an. Die Breite sollte eine ungerade Zahl sein. Ansonsten ist das Intervall unsymmetrisch und es wird rechts vom Zentrum ein Wert mehr als links davon in die Berechnung einbezogen. Erlaubte Datenstrukturen sind Einzelwert. Es sind alle ganzzahligen Datentypen erlaubt. Der Wert muss größer gleich 1 sein. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Das Ergebnis ist immer vom Datentyp 64-Bit Fließkomma.
Der absolute Variationskoeffizient einer Stichprobe ist definiert als:
![]()
Der relative Variationskoeffizient einer Stichprobe ist definiert als:
![]()
mit dem Mittelwert
![]()
und der Standardabweichung
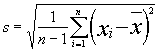
Bei Signalen und Signalreihen wird die Y-Komponente verarbeitet und die X- bzw. Z-Komponente nach Möglichkeit übernommen. Bei der Berechnung von gleitenden und Blockkoeffizienten entspricht die Datenstruktur des Ergebnisses der des Argumentes. Wenn ansonsten DataSet eine Datenreihe oder ein Signal ist, ist das Ergebnis ein Einzelwert mit dem gesuchten Variationskoeffizient, andernfalls ist das Ergebnis eine Datenreihe bzw. ein Signal mit einem Variationskoeffizient pro Spalte bzw. Zeile.
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
CoefficientOfVariation({100, 100, 100}) |
Ergibt 0. Der Datensatz mit konstanten Werten hat die Standardabweichung 0 und die Mittelwert 100 was einen Variationskoeffizienten von 0 / 100 = 0 ergibt. |
CoefficientOfVariation({90, 100, 110}) |
Ergibt 0.1. Der Datensatz mit höherer Variabilität hat die Standardabweichung 10 und die Mittelwert 100 was einen Variationskoeffizienten von 10 / 100 = 0.1 ergibt. |
CoefficientOfVariation({1, 5, 6, 8, 10, 40, 65, 88}) |
Ergibt 1.18042521004003. Der Datensatz mit noch höherer Variabilität ergibt einen noch höheren Koeffizienten. |
CoefficientOfVariation({1, 5, 6, 8, 10, 40, 65, 88}, CV_RELATIVE) |
Ergibt 0.4461587924395862. Entspricht CoefficientOfVariation({1, 5, 6, 8, 10, 40, 65, 88}) / Sqrt(7). |
CoefficientOfVariation({{90, 100, 110}, {990, 1000, 1010}}, PROCESS_COLUMNS) |
Ergibt {0.1, 0.01}. |
CoefficientOfVariation({{90, 990}, {100, 1000}, {110, 1010}}) |
Ergibt {0.1, 0.01}. |
CoefficientOfVariation({90, 100, 110, 100, 90}, CALC_MOVING, 3) |
Ergibt { 0.0744322927564787, 0.1, 0.05587260669577074, 0.1, 0.0744322927564787 }. Die Funktion berechnet den Variationskoeffizienten für {90, 100}, {90, 100, 110}, {100, 110, 100}, {110, 100, 90} und {100, 90}. |
CoefficientOfVariation({90, 100, 110, 990, 1000, 1010}, CALC_BLOCK, 3) |
Ergibt { 0.1, 0.01 }. Die Funktion berechnet den Variationskoeffizienten für die Blöcke {90, 100, 110} und {990, 1000, 1010}. |
Siehe auch
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen