Approximation (FPScript)
Approximiert ein lineares Modell Y(X) an gegebene Daten nach der Methode der kleinsten Fehlerquadrate.
Syntax
Approximation(DataSet, Model)
oder
Approximation(Amplitude, Time, Model)
Die Syntax der Approximation-Funktion besteht aus folgenden Teilen:
Teil |
Beschreibung |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
DataSet |
Das Signal oder die Datenreihe, deren Approximation berechnet wird. Wenn Sie eine Datenreihe angeben, wird die X-Komponente automatisch generiert. Erlaubte Datenstrukturen sind Datenreihe und Signal. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird die Funktion für jedes Element der Liste ausgeführt und das Ergebnis ist ebenfalls eine Liste. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Amplitude |
Eine Datenreihe mit der Y-Komponente eines Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe und Signal. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Time |
Eine Datenreihe mit der X-Komponente eines Signals. Wenn Sie ein Signal angeben, wird dessen Y-Komponente verwendet. Erlaubte Datenstrukturen sind Datenreihe und Signal. Es sind alle numerischen Datentypen erlaubt. Bei komplexen Datentypen erfolgt eine Betragsbildung. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Model |
Bestimmt den Aufbau der Modellfunktion, deren Koeffizienten durch die Approximation ermittelt werden. Sie können benutzerdefinierte oder vordefinierte Elementfunktionen angeben.
Die benutzerdefinierte Modellfunktion wird als Datenreihe von Zeichenketten übergeben. Zum Beispiel wird die Modellfunktion Y = A + B * X + C * sin(2 * PI * X) durch die Datenreihe {"1", "X", "sin(2*PI*X)"} beschrieben.
Die Modellfunktion mit vordefinierten Elementfunktionen kann durch Addition der folgenden Werte gebildet werden. Wenn z. B. die gewünschte Modellfunktion A + B * X + C * X2 lautet, so muss das Argument Model den Wert APPROX_C + APPROX_X + APPROX_X_2 erhalten. Approximation berechnet dann die unbekannten Koeffizienten A, B und C so, dass die Modellfunktion das angegebene Signal bestmöglich approximiert.
Erlaubte Datenstrukturen sind Einzelwert und Datenreihe. Unterstützte Datentypen sind 16-Bit Ganzzahl, 32-Bit Ganzzahl und Zeichenkette. Ist das Argument eine Liste, dann wird deren erstes Element entnommen. Ist dies wieder eine Liste, dann wird der Vorgang wiederholt. |
Anmerkungen
Als Ergebnis liefert die Funktion eine Datenreihe vom Datentyp 64-Bit Fließkomma.
Die Werteanzahl entspricht der Anzahl der Elementfunktionen der Modellfunktion plus Eins.
Der letzte Wert stellt das Anpassungsmaß Χ2 (Chi-Quadrat) dar. Dies ist die Summe der Quadrate aller Abweichungen der approximierten Modellfunktion von den Daten. Je kleiner Χ2 ist, desto besser approximiert die gefundene Modellfunktion die Daten. Die anderen Werte der Datenreihe liefern die Koeffizienten der in der Modellfunktion verwendeten Elementfunktionen, wobei die Reihenfolge der in obiger Tabelle verwendeten entspricht.
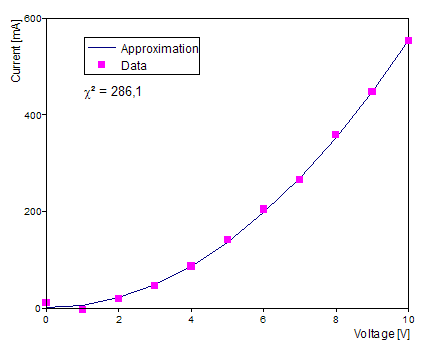
Folgende Grafik zeigt Messdaten einer quadratischen Kennlinie und deren Approximation:
Verfügbarkeit
FlexPro Basic, Professional, Developer Suite
Beispiele
Dim _c = Approximation(Signal, APPROX_C + APPROX_X + APPROX_X_2)
Signal(_c[0] + _c[1] * (Signal.X) + _c[2] * (Signal.X)^2., Signal.X)
Approximiert ein Signal mit einer quadratischen Modellfunktion.
Dim _c = Approximation(Signal, {"1", "sin(2*PI*X)"})
Signal(_c[0] + _c[1] * sin(2 * PI * Signal.X), Signal.X)
Approximiert ein Signal mit einer benutzerdefinierten Modellfunktion Y(X) = A + B * Sin(2*PI*X) .
Siehe auch
Analyseobjekt 2D-Approximation
Literatur
[1] "Philip R. Bevington, D. Keith Robinson": "Data Reduction and Error Analysis for the Physical Sciences, 3rd Edition". "McGraw-Hill, New Jork",2003.ISBN 0-07-247227-8.
Diese Beiträge könnten Sie ebenfalls interessieren
Sie sehen gerade einen Platzhalterinhalt von Facebook. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie müssen den Inhalt von reCAPTCHA laden, um das Formular abzuschicken. Bitte beachten Sie, dass dabei Daten mit Drittanbietern ausgetauscht werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von Instagram. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr InformationenSie sehen gerade einen Platzhalterinhalt von X. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Mehr Informationen